Анализ социальных сетей/Ключевые понятия
(→Анализ сплоченных подгрупп) |
(орфография, оформление) |
||
| (не показана 21 промежуточная версия 1 участника) | |||
| Строка 4: | Строка 4: | ||
* '''Личные сети'''. Сети друзей-друзей-друзей - [http://ru.wikipedia.org/wiki/Непотизм Непотизм] - семейственность. | * '''Личные сети'''. Сети друзей-друзей-друзей - [http://ru.wikipedia.org/wiki/Непотизм Непотизм] - семейственность. | ||
* [[Социальный капитал]]. | * [[Социальный капитал]]. | ||
| + | * [[Социограмма]] | ||
Традиционно для обозначения отдельного элемента социальной сети используют понятие «узел», если речь идет об исследованиях прикладного математического характера, или «актор», если подразумевается социологические исследования. В целом узел и актор по сути представляет собой отдельного человека (в социальных сетях), выступающего субъектом связей с другими индивидами. | Традиционно для обозначения отдельного элемента социальной сети используют понятие «узел», если речь идет об исследованиях прикладного математического характера, или «актор», если подразумевается социологические исследования. В целом узел и актор по сути представляет собой отдельного человека (в социальных сетях), выступающего субъектом связей с другими индивидами. | ||
=== Сетевые метрики === | === Сетевые метрики === | ||
| − | Показатели, которые используются при анализе социальных сетей. | + | Показатели, которые используются при анализе социальных сетей. См. [[Сетевые метрики]] - [[таблица]] |
==== Плотность ==== | ==== Плотность ==== | ||
| − | Плотность – это отношение числа имеющихся рёбер графа к максимально возможному количеству рёбер данного | + | Плотность – это отношение числа имеющихся рёбер графа к максимально возможному количеству рёбер данного [[граф]]а. Плотность – распространённая метрика, она используется в первую очередь при сравнении графов одного размера, или при сравнении графа с самим собой во времени. Вычисляется она по формуле: |
| − | D = n | + | D = n существующих связей/n максимально возможных |
| − | + | 2 * L / (g * (g - 1 )) - где L - число связей, а g - число вершин в графе | |
| − | + | ||
| − | + | Например, если в системе 924 участника и между ними установлены 2561 связь, то плотность равна | |
| − | + | ||
| − | + | (2 * 2561) / (924 * 923) = 0.006005731357844034 | |
| − | + | Для NetLogo в ситуации, когда есть участники и связи между ними, рассчитывается по формуле | |
| − | + | to-report density | |
| + | if count users > 2 [ report (2 * count links) / ( (count users) * ( (count users) - 1) )] | ||
| + | report 0 | ||
| + | end | ||
| − | + | ==== Коэффициент кластеризации ==== | |
| + | {{:Коэффициент кластеризации}} | ||
| + | ===== Biconnected component - компонента сильной связности ===== | ||
| − | |||
| − | + | nw:bicomponent-clusters | |
| − | + | Возвращает список бикомпонентных кластеров в текущем сетевом контексте. Бикомпонента (a maximal biconnected subgraph)- часть сети, которая не может быть разъединена благодаря удалению только одного связующего узла (шарнира). Чтобы рассыпать граф необходимо удалить хотя бы 2 узла. Бикомпонента (Strongly connected component) — максимальный по включению вершин сильно связный подграф орграфа. | |
| − | + | Reports the list of bicomponent clusters in the current network context. A bicomponent (also known as is a part of a network that cannot be disconnected by removing only one node (i.e. you need to remove at least two to disconnect it). The result is reported as a list of agentsets, in random order. Note that one turtle can be a member of more than one bicomponent at once. | |
| − | + | В исследовании школьной сети с GoogleApps было выделено 2 заметных бикомпоненты: | |
| − | + | В первой бикомпоненте более 280 узлов | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | [[Файл:Bicomponent-clusters.png|frame|В первом бикомпоненте более 280 узлов]] | ||
| − | + | Во второй бикомпоненте только 6 узлов и здесь проще читается основное правило сильной бикомпоненты - все узлы внутри бикомпоненты связаны более чем с одним узлом и нет узла, удаление которого привело бы к утрате связей между акторами сети. | |
| − | + | [[Файл:Bicomponent-clusters2.png]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===== Компонента слабой связности ===== | ===== Компонента слабой связности ===== | ||
| Строка 75: | Строка 64: | ||
==== Близость - Closeness ==== | ==== Близость - Closeness ==== | ||
Мера скорости передачи информации. Как долго будет происходить передача информации от данного узла к другим связанным узлам. | Мера скорости передачи информации. Как долго будет происходить передача информации от данного узла к другим связанным узлам. | ||
| − | Инверсия суммы кратчайших расстояний между каждым узлом и каждым другим узлом в сети. Близость показывает, насколько просто одному узлу связаться с другим узлом. Чем меньше узлов-посредников между текущем узлом и другими узлами, тем ниже показатель близости и выше степень близости.Если узел централен, то он может быстро взаимодействовать с другими узлами. | + | Инверсия суммы кратчайших расстояний между каждым узлом и каждым другим узлом в сети. Близость показывает, насколько просто одному узлу связаться с другим узлом. Чем меньше узлов-посредников между текущем узлом и другими узлами, тем ниже показатель близости и выше степень близости. Если узел централен, то он может быстро взаимодействовать с другими узлами. |
==== Центральность (Близость к центру) ==== | ==== Центральность (Близость к центру) ==== | ||
| Строка 138: | Строка 127: | ||
===== Мера центральности по собственному вектору eigenvector-centrality ===== | ===== Мера центральности по собственному вектору eigenvector-centrality ===== | ||
| − | + | ||
nw:eigenvector-centrality | nw:eigenvector-centrality | ||
| Строка 169: | Строка 158: | ||
; A clique is a subset of a network in which every node has a direct link to every other node. A maximal clique is a clique that is not, itself, contained in a bigger clique. | ; A clique is a subset of a network in which every node has a direct link to every other node. A maximal clique is a clique that is not, itself, contained in a bigger clique. | ||
| + | Клика, которая не является подмножеством более крупной клики. | ||
| + | |||
| + | Как достать клику размером больше N ? | ||
| + | show count turtle-set filter [count ? > 4] nw:maximal-cliques ;; = Сколько участников входит в клики размером от 5 ? | ||
| + | ask turtle-set filter [count ? > 4] nw:maximal-cliques [set size 2] ;; всем, кто входит в клики от 5 агентов | ||
| + | foreach filter [count ? > 4] nw:maximal-cliques [ask ? [bank_color]] | ||
| + | |||
| + | [[Файл:Pro eco max5 cliques.png]] | ||
| + | |||
| + | |||
| + | Очень показательная картинка, где в центре основная клика цветом 93. | ||
===== biggest-maximal-cliques ===== | ===== biggest-maximal-cliques ===== | ||
| Строка 174: | Строка 174: | ||
; nw:biggest-maximal-cliques | ; nw:biggest-maximal-cliques | ||
: The biggest maximal cliques are, as the name implies, the biggest cliques in the current context. Often, more than one clique are tied for the title of biggest clique, so the result if reported as a list of agentsets, in random order. If you want only one clique, use one-of nw:biggest-maximal-cliques. | : The biggest maximal cliques are, as the name implies, the biggest cliques in the current context. Often, more than one clique are tied for the title of biggest clique, so the result if reported as a list of agentsets, in random order. If you want only one clique, use one-of nw:biggest-maximal-cliques. | ||
| + | |||
| + | |||
| + | Получено по команде | ||
| + | foreach nw:biggest-maximal-cliques [ask ? [bank_color] ] | ||
| + | |||
| + | [[Файл:Sber cliques.png]] | ||
| + | |||
| + | Далее мы удаляем всех остальных участников и показываем клики | ||
| + | |||
| + | [[Файл:Sber cliques3.png]] | ||
==== Мосты (Bridges) ==== | ==== Мосты (Bridges) ==== | ||
| − | + | {{:Мост}} | |
==== Анализ социальных сетей в Интернете ==== | ==== Анализ социальных сетей в Интернете ==== | ||
Текущая версия на 01:55, 21 октября 2020
Содержание |
[править] Общие понятия
- Вероятность связывания новых узлов к существующим узлам определяется тем, сколько узлов уже связаны с данным узлом. Другими словами, богатые узлы становятся богаче.
- В большинстве реальных сетей тесно связанные группы связаны между собой через мосты.
- Личные сети. Сети друзей-друзей-друзей - Непотизм - семейственность.
- Социальный капитал.
- Социограмма
Традиционно для обозначения отдельного элемента социальной сети используют понятие «узел», если речь идет об исследованиях прикладного математического характера, или «актор», если подразумевается социологические исследования. В целом узел и актор по сути представляет собой отдельного человека (в социальных сетях), выступающего субъектом связей с другими индивидами.
[править] Сетевые метрики
Показатели, которые используются при анализе социальных сетей. См. Сетевые метрики - таблица
[править] Плотность
Плотность – это отношение числа имеющихся рёбер графа к максимально возможному количеству рёбер данного графа. Плотность – распространённая метрика, она используется в первую очередь при сравнении графов одного размера, или при сравнении графа с самим собой во времени. Вычисляется она по формуле:
D = n существующих связей/n максимально возможных
2 * L / (g * (g - 1 )) - где L - число связей, а g - число вершин в графе
Например, если в системе 924 участника и между ними установлены 2561 связь, то плотность равна
(2 * 2561) / (924 * 923) = 0.006005731357844034
Для NetLogo в ситуации, когда есть участники и связи между ними, рассчитывается по формуле
to-report density if count users > 2 [ report (2 * count links) / ( (count users) * ( (count users) - 1) )] report 0 end
[править] Коэффициент кластеризации
Кластеризация – это локальная характеристика сети. Она характеризует степень взаимодействия между собой ближайших соседей данного узла. В большинстве сетей, если узел А соединен с узлом В, а узел В – с узлом С, то существует большая вероятность, что узел А соединен с узлом С (друзья наших друзей обычно также являются и нашими друзьями).
Коэффициент кластеризации данного узла есть вероятность того, что два ближайших соседа этого узла сами есть ближайшие соседи.
Коэффициент С соответствует отношению реального числа связей между его соседями и их потенциально возможного числа. Для узла i Ci = Ei/[ki(ki-1)/2], где Ei реальное число связей, ki – степень узла, а в знаменателе записано суммарное число потенциально возможных связей между непосредственными соседями узла i (при котором сеть или еѐ часть превращается в полный граф).
Коэффициент кластеризации может быть усреднен для любой части сети или для сети в целом, становясь ее интегральной характеристикой: C = 1/n ΣCi.
Усредненный коэффициент кластеризации для групп участников школьной сети. Если мы можем по какому либо принципу выделить группу участников, то мы можем определить коэффициент кластеризации в пределах данной группы. Для членов устойчивой группы - клики - коэффициент кластеризации = 1.
Коэффициент кластеризации – это метрика, которая является более эффективной, чем плотность, и её всё чаще используют в общественных науках. Коэффициент кластеризации – степень, определяющая насколько узлы стремятся к кластеризации. Например, в сети друзей это вероятность того, что 2 моих друга являются друзьями между собой. То есть это некоторая оценка фрагментированности сети. При высокой кластеризации можно ожидать, что вирус будет распространяться лишь в определенной подгруппе (кластере). При низкой кластеризации высока вероятность быстрого распространения вируса по всей сети
[править] Локальный коэффициент кластеризации
Коэффициент локального объединения в кластеры (коэффициент кластеризации) является мерой того, насколько хорошо связанны связаны между собой соседи данного узла. Локальный коэффициент кластеризации рассчитывается как число связей межу соседями данного узла / возможное число связей между соседями.
NetLogo позволяет рассчитывать
turtle nw:clustering-coefficient - local clustering coefficient of the turtle.
Reports the local clustering coefficient of the turtle. The clustering coefficient of a node measures how connected its neighbors are. It is defined as the number of links between the node's neighbors divided by the total number of possible links between its neighbors.
nw:clustering-coefficient takes the directedness of links into account. A directed link counts as a single link whereas an undirected link counts as two links (one going one-way, one going the other).
Мы всегда рассматриваем ситуацию как сравнение числа существующих связей к числу возможных связей. Есть узлы, все соседи которых связаны между собой. Есть узлы между соседями которых вообще нет никаких связей. И опять это ситуация, когда есть развитая сеть и все соседи связаны между собой - это сообщество, это клика, где все друг с другом связаны.
Чем выше локальный коэффициент кластеризации, тем выше вероятность того, что участник данный участник входит в состав устойчивой группы и обладает социальными компетенциями, необходимыми для использования объектов, созданные другими участниками, и создания объектов, нужных другим участникам.
Закономерности: - Закон Меткалфа
Если рассматривать ценность сети с педагогической точки зрения - как создание устойчивых связей между всеми акторами сети, то для отдельного участника число его связей с другими участниками / на возможное число связей.
[править] Глобальный коэффициент кластеризации
Коэффициент кластеризации – это значения кластеризации для всех узлов графа. Когда коэффициент кластеризации высокий – это означает, что граф чрезвычайно плотно сгруппирован вокруг нескольких узлов; когда он низкий – это значит, что связи в графе относительно равномерно распространены среди всех узлов.
Вычисляется на основании того сколько треугольников сложено в сети от возможного количества треугольников. Например, на следующей картинке коэффициент кластеризации равен 1/3 - потому что там моглор бы быть 3 треугольника, а сложился только 1

The global clustering coefficient measures how much nodes tend to cluster together in the network in general. It is defined based on the types of triplets in the network. A triplet consists of a central node and two of its neighbors. If its neighbors are also connected, it's a closed triplet. If its neighbors are not connected, it's an open triplet. The global clustering coefficient is simply the number of closed triplets in a network divided by the total number of triplets. It can be calculated from the local clustering coefficient quite easily with the following code
to-report global-clustering-coefficient let closed-triplets sum [ nw:clustering-coefficient * count my-links * (count my-links - 1) ] of turtles let triplets sum [ count my-links * (count my-links - 1) ] of turtles report closed-triplets / triplets end
transitivity(g, type="local") order(transitivity(g, type="local"))
Насколько узлам свойственно объединяться в кластеры
Усредненный коэффициент кластеризации - The average local clustering coefficient is another popular method for measuring the amount of clustering in the network as a whole. It may be calculated with
mean [ nw:clustering-coefficient ] of turtles
[править] Biconnected component - компонента сильной связности
nw:bicomponent-clusters
Возвращает список бикомпонентных кластеров в текущем сетевом контексте. Бикомпонента (a maximal biconnected subgraph)- часть сети, которая не может быть разъединена благодаря удалению только одного связующего узла (шарнира). Чтобы рассыпать граф необходимо удалить хотя бы 2 узла. Бикомпонента (Strongly connected component) — максимальный по включению вершин сильно связный подграф орграфа.
Reports the list of bicomponent clusters in the current network context. A bicomponent (also known as is a part of a network that cannot be disconnected by removing only one node (i.e. you need to remove at least two to disconnect it). The result is reported as a list of agentsets, in random order. Note that one turtle can be a member of more than one bicomponent at once.
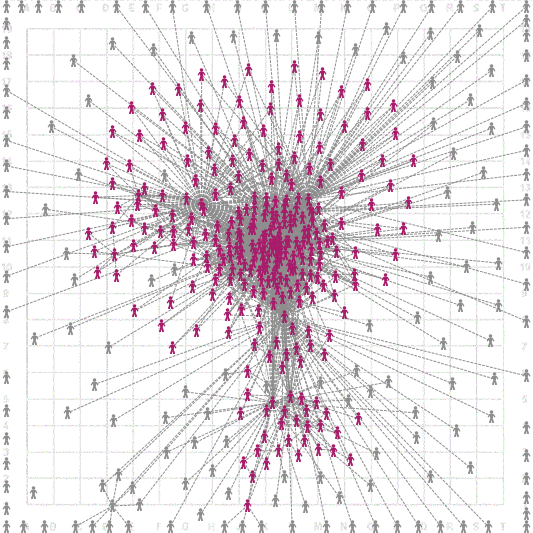
В исследовании школьной сети с GoogleApps было выделено 2 заметных бикомпоненты:
В первой бикомпоненте более 280 узлов
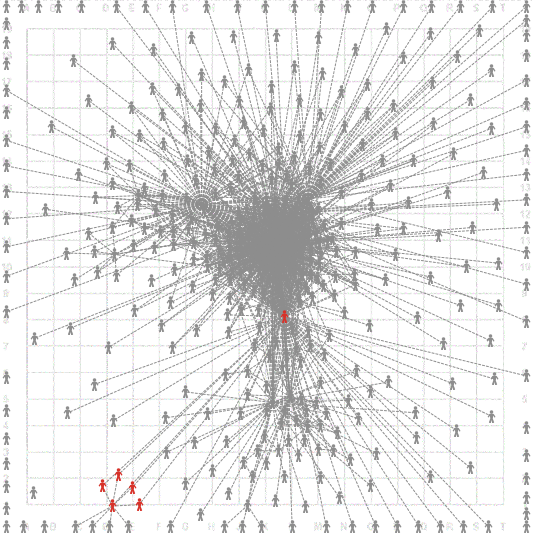
Во второй бикомпоненте только 6 узлов и здесь проще читается основное правило сильной бикомпоненты - все узлы внутри бикомпоненты связаны более чем с одним узлом и нет узла, удаление которого привело бы к утрате связей между акторами сети.
[править] Компонента слабой связности
nw:weak-component-clusters
Reports the list of "weakly" connected components in the current network context. A weakly connected component is simply a group of nodes where there is a path from each node to every other node. A "strongly" connected component would be one where there is a directed path from each node to every other. The extension does not support the identification of strongly connected components at the moment.
The result is reported as a list of agentsets, in random order. Note that one turtle cannot be a member of more than one weakly connected component at once.
[править] Degree
Количество узлов, связанных с данным узлом - степень данного узла.
[править] Близость - Closeness
Мера скорости передачи информации. Как долго будет происходить передача информации от данного узла к другим связанным узлам. Инверсия суммы кратчайших расстояний между каждым узлом и каждым другим узлом в сети. Близость показывает, насколько просто одному узлу связаться с другим узлом. Чем меньше узлов-посредников между текущем узлом и другими узлами, тем ниже показатель близости и выше степень близости. Если узел централен, то он может быстро взаимодействовать с другими узлами.
[править] Центральность (Близость к центру)
Для анализа связей в социальной сети используют различные индивидуальные и групповые показатели, позволяющие оценить степень заметности и влияния акторов друг на друга. Собственно идея центральности вершин в графе, их значения появилась одной из первых в методологии анализа социальных сетей, и напрямую может быть увязана с первыми попытками Дж. Морено выявить самых популярных участников в группе («социометрических звезд»). Позднее эта мера заметности актора в сети стала называться центральностью.
Близость к центру или Степень центральности (Degree centrality) – показывает, кто является наиболее активным узлом в сети. Измеряется количеством связей с другими узлами в сети. Центральность показывает, насколько данный узел близок по отношению к другим узлам в сети. В соответствие с теорией сетей большое количество взаимодействий узла может не только изменить позицию узла в сети, но также и изменить позиции других узлов.
- Престиж узла: входная степень узла (in-degree) — количество ребер графа, входящих в узел.
- Влияние узла: выходная степень узла (out-degree) — количество ребер графа, исходящих из узла. Эта характеристика показывает, кто является наиболее активным в сети. Индивидуальный показатель близости к центру показывает, в какой степени узел связан остальными узлами, то есть насколько тесно он связан с группой.
- Freeman L.C. Centrality in social networks: Conceptual clarification // Social Networks. 1979. Т. 1. № 3. С. 215–239.
Мера центральности описывает выдающееся положение конкретного узла по сравнению с другими узлами. Средняя мера центральности также известна как централизованная оценка и указывает, насколько плотен граф по отношению к каждому узлу. Есть три показателя центральности: центральность по степени, центральность по близости и центральность по посредничеству.
[править] Центральность по степени
Смысл этой меры основан на допущении, что тот, кто обладает большим количеством связей (отношений) с другими, занимает центральное положение в локальной общности.
Центральность по степени – это отношение количества связей определённого узла к общему количеству других узлов. В случае направленной сети существует две отдельных меры ЦС: входящая (indegree) и исходящая (outdegree). Входящая указывает число связей, направленных к узлу, а исходящая – число связей, направленных от узла. Если ЦС = 1, это указывает на то, что определённый узел связан со всеми остальными узлами сети, в то время как ЦС = 0 указывает на то, что узел изолирован. Так как многие интернет-сети являются направленными, есть определённый смысл в том, чтобы использовать входящую и исходящую центральность по степени. Высокая исходящая центральность по степени указывает на то, что узел является «властным»; это такой тип человека или сайта, который может быстро распространить информацию среди других людей. Высокая входящая центральность по степени указывает, что узел – «знаменитость»; это значит, что за таким типом человека или сайта будет следить много людей. Google.com имеет миллиарды внешних ссылок на другие сайты. Это – власть. YouTube.com имеет относительно немного ссылок на другие сайты, однако, много людей размещают ссылки на YouTube или встраивают его контент на собственные страницы. Это – известность.
Недостатком такой меры является то, что количество социальных контактов зачастую не отражает их качества, а просто свидетельствует о степени общительности индивида.
Если позиция, занимаемая актором-мостом, отличается высокой степенью центральности (degree centrality), то есть он имеет больше прямых связей с акторами, чем другие, он может широко распространять свои коммуникативные темы в тех сплоченных подгруппах, к которым принадлежит, тем самым внося вклад в сближение структуры и состава полей знания соответствующих РКС (распределенная когнитивная система). Чем меньше таких акторов, чем центральнее их позиция, тем больший вклад в обеспечение конгруэнтности полей знания они способны внести. Если же актор-мост в большой мере промежуточно централен (betweenness centrality), то есть чаще других находится на пути от одного актора сети к другому, он может контролировать значительное число информационных потоков между сплоченными подгруппами, членом которых является, а следовательно, ограничивать разнообразие информации. Его ошибки, намеренная дезинформация или необычные, творческие коммуникативные практики способны порождать наиболее отклоняющиеся информационные вариации в полях знания РКС. В случае, когда относительное количество таких акторов и их коммуникаций велико, они усиленно раздражают друг друга и порождают множество отклонений-новаций, а сопряжение между подгруппами сети, по-видимому, усиливается. Если же акторы скорее склонны ограничивать проходящую информацию, то сопряжение, вероятнее всего, будет ослабевать.
- Басов Н.В. Создание знания в сетевых коммуникативных структурах // Социологический журнал. 2014. № 1. С. 106–123.
[править] Центральность по близости closeness-centrality
Центральность по близости выражает, насколько близко узел расположен к остальным узлам сети. По мнению Фримана, это мера эффективности, так как узел, который является наиболее близким к остальным узлам графа, лучше всех подвержен восприятию новой информации или вируса. Формально центральность по близости выражается как отношение числа других узлов графа к сумме расстояний между определённым узлом и всеми другими. Если БЦ = 1, это означает, что определённый узел связан со всеми другими узлами. Вероятно, что сайты СМИ, которые имеют блог-платформы, такие как Gizmodo.com и DailyKOS.com имеют очень высокий показатель БЦ. Они содержат ссылки на большое количество других сайтов, и многие другие сайты, в свою очередь, ссылаются на них.
Центральность по близости (Closeness centrality) является показателем того, насколько быстро распространяется информация в сети от одного участника к остальным, то есть насколько близок рассматриваемый участник ко всем остальным участникам сети.
Показатель «центральность по близости» (closeness centrality) демонстрирует, насколько легко достичь определенного узла в сети. Если говорить о футболе, то этот показатель позволяет судить, как этот игрок взаимодействует с командой.
Суть его состоит в том, чтобы оценить насколько близок (то есть включен в непосредственное взаимодействие) актор ко всем остальным участникам сети. Для того чтобы иметь высокую степень данного вида центральности, актор должен не просто обладать множеством связей. Важно, чтобы у его друзей и партнеров тоже их было достаточно. Это означает, что актор с высокой степенью центральности по близости через те связи, в которые он включен, получает возможность доступа к большому количеству других участников сети, распространяя свое влияние на них. Не случайно так называемые влиятельные распространители информации имеют высокую степень центральности по близости. Например, если актор знает всех субъектов сети, то степень его центральности будет равна единице
The closeness centrality of a turtle is defined as the inverse of the average of it's distances to all other turtles. - Обратное среднему от расстояний до всех других черепах.
см. https://github.com/NetLogo/NW-Extension - Сетевое расширение NetLogo - и отдельный раздел о измерении центральности
Если речь идет о распространении данных и выявлении информационных потоков в организации, а исследователь заинтересован в поиске акторов, которые могут наиболее эффективно принимать и передавать их, то более всего подходит измерение центральности по близости, поскольку для получения информации нужно быть рядом с остальными. В этом случае акторы, имеющие в среднем более короткую дистанцию до других участников сети, могут наиболее эффективно передавать и получать информацию.
[править] Центральность по посредничеству betweenness-centrality
Центральность по посредничеству - вынесено в отдельную статью по причине значимости
[править] Групповые показатели центральности
Групповые показатели центральности являются мерами изменчивости или неравенства индивидуальных показателей в графе и показывают насколько различаются акторы по степени индивидуальной центральности. В таком общем понимании групповые индексы по смыслу близки дисперсии (мере разброса). По причинам математического свойства наиболее популярны групповые индексы Фримана по степени, близости или посредничеству. Каждый из этих показателей равен сумме отклонений индивидуальных показателей от максимального наблюдаемого, отнесенной к теоретически возможному максимуму сумм отклонений. Знаменатель получают аналитически. Групповые индексы равны нулю в том случае, когда все индивидуальные показатели равны, и 100, если в графе доминирует одна вершина. В отличие от дисперсии, групповые индексы не зависят от размера графа.
Для группового показателя центральности по посредничеству = Sum (maxV - Vi)/ (((N - 1)* (N - 1) * (N - 2) ) / 2)
to-report centralization let znm ((count turtles - 1) * (count turtles - 1) * (count turtles - 2)) / 2 ; let mx max [nw:betweenness-centrality] of turtles ; report (sum map [mx - ?] [nw:betweenness-centrality] of turtles ) / znm end
Групповая центральность по посредничеству в NetLogo. Групповая центральность по посредничеству позволяет сравнивать проекты совместной сетевой деятельности независимо от числа участников
[править] Мера центральности по собственному вектору eigenvector-centrality
nw:eigenvector-centrality
Центральность по собственному вектору (Eigenvector centrality) демонстрирует зависимость между центральностью участника и центральностями его друзей.
The Eigenvector centrality of a node can be thought of as the amount of influence a node has on a network. In practice, turtles that are connected to a lot of other turtles that are themselves well-connected (and so on) get a higher Eigenvector centrality score.
Черепаха, которая имеет много связей с теми, у кого тоже много связей, имеет высокую центральность по собственному вектору.
Мера центральности по собственному вектору (eigenvector centrality) еще более сложна для вычисления и возможна только с помощью специализированных компьютерных программ. Идея ее измерения основана на принципе «скажи мне, кто твой друг, и я скажу, кто ты». Здесь усилия направлены на то, чтобы найти центральных акторов (то есть с наименьшей удаленностью от других) в условиях глобальной или масштабной, сложной по структуре сети, имеющих множество подгрупп, и преодолеть ограничение моделей, более подходящих для анализа локальных сообществ и сетей.
[править] page-rank
[править] weighted-closeness-centrality
nw:weighted-closeness-centrality
[править] Анализ сплоченных подгрупп
Анализ сплоченных подгрупп. Сплоченность принадлежит к числу основных характеристик социальных групп. В широком смысле она понимается как единство, общность норм и интересов, взаимные симпатии членов группы. Основными индикаторами сплоченности в А.С.С. выступают взаимность и частота контактов акторов, близость и достижимость вершин графа. В разумно больших сетях обычно обнаруживают несколько пересекающихся сплоченных подгрупп. Для аналитика интерес представляют количество, состав, размер, а также степень взаимного пересечения подгрупп. Большинство методов этого раздела разработаны для ненаправленных дихотомических связей, и компьютерные программы анализа сетей приводят социоматрицы к симметричному виду.
Простейшим методом анализа сплоченных подгрупп является идентификация клик. В терминах теории графов это максимальный полный подграф, включающий не менее трех вершин. По определению, все вершины клики связаны между собой, и при добавлении любой другой вершины это свойство теряется. Следует иметь в виду, что в отечественной социальной психологии закрепилось определение клики как сплоченной асоциальной группировки. Понятие клики является чрезмерно строгим, а полученные подмножества акторов неустойчивы: удаление или случайное отсутствие одной связи разрушает клику. Чтобы ослабить это ограничение, были разработаны другие меры сплоченности подгрупп. Они основаны либо на понятии достижимости вершин в подграфе, либо на степени вершины (смежность с другими).
Клика порядка n (n-клика) определена как максимальный подграф, в котором наибольшее расстояние между вершинами не превышает заданной величины n. Основным недостатком этого подхода является то, что наикратчайшие пути между членами n-клики могут проходить через посредников, которые сами не принадлежат сплоченной подгруппе. Это обстоятельство может создавать трудности в интерпретации результатов. Скорректированное понятие называется кланом порядка n. Кланы получают исключением из найденных n-клик подгрупп с диметром (наибольшим из самых коротких расстояний между вершинами), превышающим заданное n. Алгоритм поиска клик и кланов заданного порядка обычно приводит к большим подгруппам.
[править] maximal-cliques
- nw:maximal-cliques
- A clique is a subset of a network in which every node has a direct link to every other node. A maximal clique is a clique that is not, itself, contained in a bigger clique.
Клика, которая не является подмножеством более крупной клики.
Как достать клику размером больше N ?
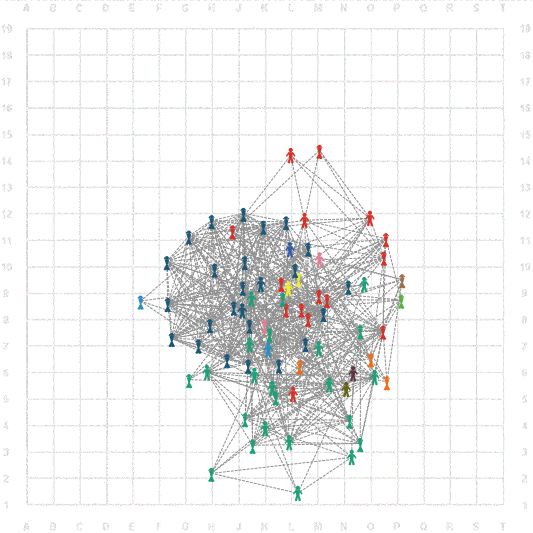
show count turtle-set filter [count ? > 4] nw:maximal-cliques ;; = Сколько участников входит в клики размером от 5 ? ask turtle-set filter [count ? > 4] nw:maximal-cliques [set size 2] ;; всем, кто входит в клики от 5 агентов foreach filter [count ? > 4] nw:maximal-cliques [ask ? [bank_color]]
Очень показательная картинка, где в центре основная клика цветом 93.
[править] biggest-maximal-cliques
- nw
- biggest-maximal-cliques
- The biggest maximal cliques are, as the name implies, the biggest cliques in the current context. Often, more than one clique are tied for the title of biggest clique, so the result if reported as a list of agentsets, in random order. If you want only one clique, use one-of nw:biggest-maximal-cliques.
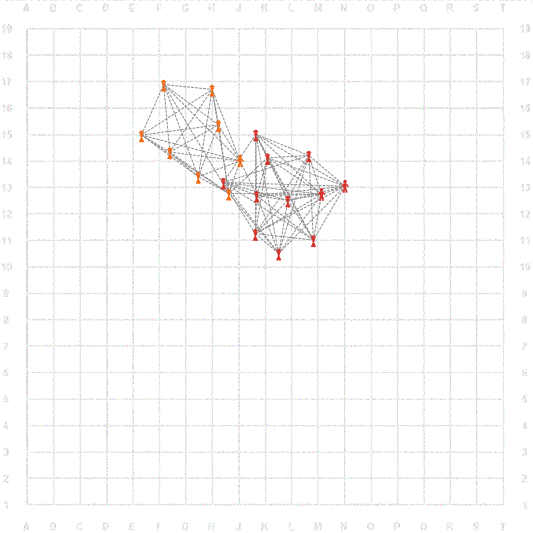
Получено по команде
foreach nw:biggest-maximal-cliques [ask ? [bank_color] ]
Далее мы удаляем всех остальных участников и показываем клики
[править] Мосты (Bridges)
Мост — ребро в теории графов, удаление которого увеличивает число компонент связности. Такие рёбра также известны как разрезающие рёбра, разрезающие дуги или перешейки. Эквивалентное определение — ребро является мостом в том и только в том случае, если оно не содержится ни в одном цикле. Узел соединяющий отдельные части сети называется мостом. Удаление моста разрывает структуру и приводит к росту отдельных узлов. Поиск узлов помогает в понимании наиболее важных отношений и независимых групп.
[править] Анализ социальных сетей в Интернете
- Анализ социальных сетей в интернете - Берни Хоган
- Hogan, B., Carrasco, J., & Wellman, B. (2007). Visualizing personal networks: Working with participant aided sociograms. Field Methods, 19(2), 116-144.
[править] Литература
- Коулман Дж. Капитал социальный и человеческий // Общественные науки и современность. – 2001. - № 3. – С. 121 – 139.
- Freeman L.C., White D.R., Romney A.K. Research methods in social network analysis. Transaction Publishers, 1992. 544 с.
- Wenger E., McDermott R.A., Snyder W. Cultivating Communities of Practice: A Guide to Managing Knowledge. : Harvard Business Press, 2002. 306 с.