Модели взаимодействия в мультиагентных средах
м |
|||
| (не показаны 9 промежуточных версий 4 участников) | |||
| Строка 8: | Строка 8: | ||
{{Шаблон:Править название}} | {{Шаблон:Править название}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Строка 130: | Строка 158: | ||
Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955—1956гг. | Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955—1956гг. | ||
| − | |||
| − | |||
| − | |||
| − | |||
Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т. е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины' вручную—очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ. | Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т. е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины' вручную—очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ. | ||
Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. | Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. | ||
Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас». | Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас». | ||
Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс — явно немарковскпй, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным). | Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс — явно немарковскпй, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным). | ||
| − | |||
| − | |||
| − | |||
В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 — (1/2)3 = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб—за попадание, решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен. | В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 — (1/2)3 = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб—за попадание, решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен. | ||
| Строка 314: | Строка 335: | ||
'''Мультиагентные системы в логистике и е-коммерции.''' | '''Мультиагентные системы в логистике и е-коммерции.''' | ||
Всемирная экономика характеризуется частой сменой спроса на ресурсы, что оказывает определенное давление на производителей, которые поставляют свои товары в разные части света. Закупка мест в грузовом самолете, наем автотранспорта, аренда складских помещений, мониторинг потоков запчастей и оборудования и своевременная доставка " деловые операции, еще более трудно осуществимые теперь, чем когда-либо. Даже изнутри процесса, в рамках предприятия, логистика становится кошмаром из-за того, что покупатели часто пользуются своим правом передумать насчет параметров и характеристик своих покупок. | Всемирная экономика характеризуется частой сменой спроса на ресурсы, что оказывает определенное давление на производителей, которые поставляют свои товары в разные части света. Закупка мест в грузовом самолете, наем автотранспорта, аренда складских помещений, мониторинг потоков запчастей и оборудования и своевременная доставка " деловые операции, еще более трудно осуществимые теперь, чем когда-либо. Даже изнутри процесса, в рамках предприятия, логистика становится кошмаром из-за того, что покупатели часто пользуются своим правом передумать насчет параметров и характеристик своих покупок. | ||
| − | Современные системы логистики централизованы и оптимизированы под поставку товаров "на поток?, в стабильной ситуации, следовательно, слишком негибки чтобы справиться со сложными, постоянно меняющимися внешним и внутренним потоками материалов. Производители машин в настоящее время ежегодно теряют миллионы долларов из-за негибкости своих централизованных систем материально-технического снабжения. | + | Современные системы логистики централизованы и оптимизированы под поставку товаров "на поток?, в стабильной ситуации, следовательно, слишком негибки чтобы справиться со сложными, постоянно меняющимися внешним и внутренним потоками материалов. Производители машин в настоящее время ежегодно теряют миллионы долларов из-за негибкости своих централизованных систем материально-технического снабжения. |
| − | + | ||
| − | + | ||
| − | + | ||
Первая разработка компании "МАГЕНТА" в области мультиагентной логистики органично связана с е-коммерцией и будет описана далее на примере ее использования в автомобильном бизнесе - торговле, управлении системой распределения и снабжения. | Первая разработка компании "МАГЕНТА" в области мультиагентной логистики органично связана с е-коммерцией и будет описана далее на примере ее использования в автомобильном бизнесе - торговле, управлении системой распределения и снабжения. | ||
Используя стандартные способы предсказания спроса, производитель машин планирует производство ряда автомобилей, каждый из которых обладает набором возможного оборудования. Это - Запланированные машины. Дилеры (или, напрямую, покупатели) подают заявки на машины, указывая модель и параметры. Это - Заказанные машины. Каждая Запланированная машина также уже расписана, и агент обязан найти соответствующую Заказанную машину. Агенты взаимодействуют и легко находят подходящую пару машин. Запланированные и Заказанные машины, не нашедшие пару, уходят на второй раунд переговоров, которые, возможно, будут включать предложения о скидках или дополнительной плате для облегчения поиска подходящей пары. Современная практика разрешает покупателям изменять спецификацию заказанного автомобиля даже после того, как заказ был запущен в производство. Агент, занимающийся такой машиной, должен позаботиться, чтобы изменения были приняты во внимание, и внутренние производственные процессы были соответственно модифицированы. Такой же процесс согласования купленных машин и средств для их транспортировки должен происходить в Портале 2, как только процесс купли-продажи в Портале 1 завершен. В Портале 3 агенты должны соотносить машины и соответствующие детали и организовывать распределение деталей для конвейеров и цехов сборки машин. | Используя стандартные способы предсказания спроса, производитель машин планирует производство ряда автомобилей, каждый из которых обладает набором возможного оборудования. Это - Запланированные машины. Дилеры (или, напрямую, покупатели) подают заявки на машины, указывая модель и параметры. Это - Заказанные машины. Каждая Запланированная машина также уже расписана, и агент обязан найти соответствующую Заказанную машину. Агенты взаимодействуют и легко находят подходящую пару машин. Запланированные и Заказанные машины, не нашедшие пару, уходят на второй раунд переговоров, которые, возможно, будут включать предложения о скидках или дополнительной плате для облегчения поиска подходящей пары. Современная практика разрешает покупателям изменять спецификацию заказанного автомобиля даже после того, как заказ был запущен в производство. Агент, занимающийся такой машиной, должен позаботиться, чтобы изменения были приняты во внимание, и внутренние производственные процессы были соответственно модифицированы. Такой же процесс согласования купленных машин и средств для их транспортировки должен происходить в Портале 2, как только процесс купли-продажи в Портале 1 завершен. В Портале 3 агенты должны соотносить машины и соответствующие детали и организовывать распределение деталей для конвейеров и цехов сборки машин. | ||
| Строка 428: | Строка 446: | ||
- с формированием образовательного маршрута (отбор выпускников любых направлений подготовки бакалавриата с учетом недостающих дисциплин и их освоения в процессе обучения в магистратуре). | - с формированием образовательного маршрута (отбор выпускников любых направлений подготовки бакалавриата с учетом недостающих дисциплин и их освоения в процессе обучения в магистратуре). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 15:15, 6 апреля 2016
В названии страницы надо указать, чья работа
| Статью необходимо переименовать- см. Имя статьи |
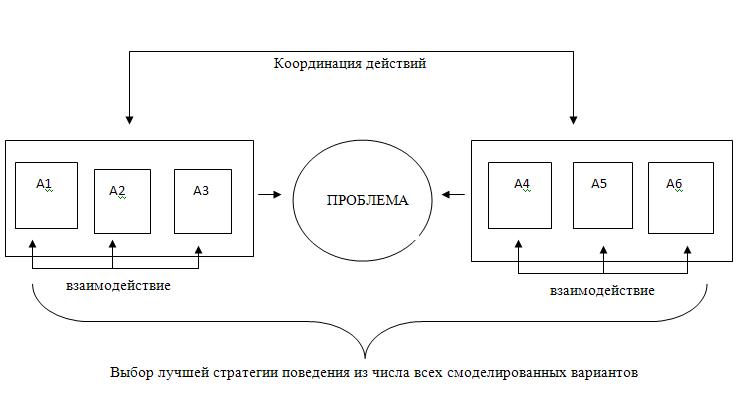
Мультиагентное моделирование при принятии управленческого решения. Мультиагентное моделирование является эффективным средством нахождения оптимального решения задач, принятия управленческого решения. В этом контексте та или иная ситуация проецируется на искусственно созданную модель, где каждый агент наделяется определенным функционалом. В управленческой среде речь может идти о моделировании ситуации, где задействованы люди, производственные процессы, объекты и прочее. Живые агенты — люди — имеют одно отличительное свойство по сравнению с другими агентами (роботы, компьютерные агенты). Это свойство — социальность. В таких моделях важно учитывать социальный статус, социальные отношения, распределение функций, наделение полномочиями. Агентные системы, смоделированные по образу человеческого сообщества, связаны с теорией организацией, теорией административного управления, теорией игр и др. Однако, в таких системах очень тяжело учесть ценностные ориентиры, которые приняты в данной группе. Люди могут выбрать нормативную и ненормативную линию поведения, что нельзя никак перенести на агент. Но в остальном агенты также могут обращаться к другим агентам при решении поставленной задачи, строить совместные планы, координировать свои действия. Такой подход к решению задачи очень удобен, он отсекает много рисков. Например, он позволяет руководителю выбрать правильную стратегию поведения во взаимоотношениях с поставщиками, клиентами, конкурентами, в кризисной ситуации ограниченности ресурсов. Если резюмировать, то при моделировании мультиагентных сред важно учитывать: 1. Отражение особенностей таких как, тип ресурса, с которым работают агенты (материальный, информационный, человеческий), состояние операции, проблемное поле; 2. Определение целей каждого агента, описание его знаний; 3. Описание механизма взаимодействия между агентами, группами агентов; 4. Описание механизма разрешения конфликтных ситуаций между агентами, группами агентов; 5. Описание плана действий агентов, групп агентов.
--Гнетнева Ксения (обсуждение) 13:55, 5 апреля 2016 (MSK)
Мультиагентное моделирование в среде NetLogo
Программа NetLogo обладает простым функциональным интерфейсом. Главным элементом, которого является окно «виртуального Мира» агентов. На рисунке это окно расположено в центре экрана.
Пользователь и разработчик агентной программы может взаимодействовать с ней в интерактивном режиме, подавая команды в окне «Командного центра», оно расположено в нижней части окна программы. Команды подаются на уровне определенного объекта программы моделирования: «Наблюдатель», «Пятна», «Черепахи» (агенты), «Связи». Команда — это определенный оператор языка программирования NetLogo. Допускается создание комбинированных моделей, код которых предварительно записан на языке NetLogo, и затем модель исследуется с привлечением командного центра. Код агентной модели представляет собой набор процедур. Пример на картинке:
В модели всегда должны присутствовать две процедуры setup и go [4]. Первая процедура связывается с командной кнопкой инициализации агентов модели, вторая запускает процесс моделирования. Движение агентов в виртуальном мире показано на рисунке. По умолчанию используется пиктограмма агента в виде направленного острия. Допускается сменить пиктограмму агента на другую из библиотеки ресурсов программы, либо создать собственную пиктограмму, с помощью графического редактора. Графический редактор входит в систему моделирования.
Примером модели может служить — Модель «хищник — жертва»
Такой класс моделей позволяет исследовать взаимодействие агентов в виртуальном Мире, где наблюдается конкуренция между агентами. Один класс агентов «хищники», поддерживают свой жизненный потенциал за счет уничтожения других агентов «жертв». Вид интерфейса работающей модели показан на рисунке
Агенты обоего типа обладает энергией, если она падает ниже определенного уровня, то агент «умирает». Агенты жертвы поддерживают свою энергию за счет «зеленых пятен», поглощая их, агент хищник поддерживает свою энергию за счет уничтожения жертв. Когда энергия агентов возрастает до определенного уровня, они воспроизводит себе подобных. Это операция клонирования агентов. Для контроля за состоянием ресурсов используется экран «Ресурсы». Экран отображает число ресурсов — пятен зеленого цвета, ресурсы возобновляются. Из рисунка видно, что популяции «хищников» и обычных агентов имеет пиковые значения, после численность популяции начинает стабилизироваться.
--Крашенинников Алексей (обсуждение) 21.58, 5 апреля 2016 (MSK)
Имитационное моделирование
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории – неограниченно большое) число факторов. Но и у них – свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб. Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей. Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время . Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т.д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучивается принимать правильные решения – если не оптимальные, то почти оптимальные. В современной литературе не существует единой точки зрения по вопросу о том, что понимать под имитационным моделированием. Так существуют различные трактовки: - в первой – под имитационной моделью понимается математическая модель в классическом смысле; - во второй – этот термин сохраняется лишь за теми моделями, в которых тем или иным способом разыгрываются (имитируются) случайные воздействия; - в третьей – предполагают, что имитационная модель отличается от обычной математической более детальным описанием , но критерий, по которому можно сказать, когда кончается математическая модель и начинается имитационная , не вводится;
Имитационное моделированием применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или иные решения, подобно тому, как шахматист глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки, в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее текущее решение принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные.
Этапы процесса построения математической модели сложной системы
1. Формулируются основные вопросы о поведении системы, ответы на которые мы хотим получить с помощью модели. 2. Из множества законов, управляющих поведением системы, выбираются те, влияние которых существенно при поиске ответов на поставленные вопросы. 3. В пополнение к этим законам, если необходимо, для системы в целом или отдельных ее частей формулируются определенные гипотезы о функционировании. Критерием адекватности модели служит практика.
Трудности при построении математической модели сложной системы:
- Если модель содержит много связей между элементами, разнообразные нелинейные ограничения, большое число параметров и т. д. - Реальные системы зачастую подвержены влиянию случайных различных факторов, учет которых аналитическим путем представляет весьма большие трудности, зачастую непреодолимые при большом их числе; - Возможность сопоставления модели и оригинала при таком подходе имеется лишь в начале.
Эти трудности и обуславливают применение имитационного моделирования.
Оно реализуется по следующим этапам:
1. Как и ранее, формулируются основные вопросы о поведении сложной системы, ответы на которые мы хотим получить. 2. Осуществляется декомпозиция системы на более простые части-блоки. 3. Формулируются законы и «правдоподобные» гипотезы относительно поведения как системы в целом, так и отдельных ее частей. 4. В зависимости от поставленных перед исследователем вопросов вводится так называемое системное время, моделирующее ход времени в реальной системе. 5. Формализованным образом задаются необходимые феноменологические свойства системы и отдельных ее частей. 6. Случайным параметрам, фигурирующим в модели, сопоставляются некоторые их реализации, сохраняющиеся постоянными в течение одного или нескольких тактов системного времени. Далее отыскиваются новые реализации.
Метод Монте-Карло как разновидность имитационного моделирования
Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955—1956гг. Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т. е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины' вручную—очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ. Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас». Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс — явно немарковскпй, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным). В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 — (1/2)3 = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб—за попадание, решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен.
Список литературы
1. Вентцель Е.С. «Исследование операций», Москва «Советское радио» 1972 г. 2. Соболь И.М. «Метод Монте-Карло», Москва «Наука»,1985 г. 3. «Экономико-математические методы и прикладные модели», под ред. Федосеева В.В. , Москва «Юнити» 2001 г.
Коалиционная модель мультиагентного процесса преобразования ресурсов
Целью разработки коалиционной модели мультиагентного процесса преобразования ресурсов (МППР) является описание процессов взаимодействия агентов и формирования коалиций при решении вопросов коллективного использования ресурсов и средств в условиях параллельного выполнения МППР. Разработанная модель отвечает следующим требованиям.
1. Ориентация на моделирование мультиагентных процессов преобразования ресурсов. Необходимо отражение следующих основных особенностей МППР: учет различных типов ресурсов (материальных, информационных, энергетических, трудовых, финансовых); наличие возможности задания начальных состояний операций над ресурсами; учет возникновения и разрешения конфликтов; наличие возможности иерархического представления структуры процесса и расчета различных характеристик процесса на каждом уровне иерархии.
2. Наличие возможности описания гибридных моделей агентов, в т.ч.: определение целей агента, описание базы знаний агента, выбор определенной стратегии взаимодействий агента.
3. Наличие механизма формирования коалиций, обеспечивающего следующие основные возможности: определение целей коалиции, описание базы знаний коалиции.
4. Наличие механизма описания мультиагентных систем (МАС), позволяющего определение: множества агентов и коалиций МАС, множества установленных связей между агентами и коалициями, общей базы знаний МАС.
5. Наличие аппарата организации взаимодействий агентов и коалиций, включающего: язык общения агентов, соответствующий проблемной области МППР и разработанный на основе стандарта взаимодействия агентов; механизм обмена сообщениями между агентами и коалициями и множество методов взаимодействий агентов и коалиций в МАС.
6. Наличие механизма разрешения конфликтов между агентами, основанного на использовании стратегий взаимодействий и организации аукционов.
7. Наличие механизма составления планов действий для агентов и коалиций.
Реализация вышеперечисленных требований обеспечивается с помощью применения имитационного моделирования, теории процессов преобразования ресурсов (ППР), теории мультиагентных систем, теории аукционов и теории составления расписаний.
Основой для создания коалиционной модели МППР является математическая модель, разработанная Аксеновым К.А. и Гончаровой Н.В..
Сравнение коалиционной модели с моделью И.М. Москалева
В работе И.М. Москалева представлена математическая модель ППР из пассивных преобразователей, модель из активных преобразователей и смешанная модель.
Модель активных и пассивных ППР,
где – множество активных элементов модели ППР; – множество пассивных элементов модели ППР; – хранилища ресурса; – множество разделяемых парков средств; – множество возможных потоков ресурса между элементами модели; – множество потоков средств между элементами модели; – множество информационных потоков между преобразователями; – множество ресурсов в сети.
Пассивный преобразователь может находиться в трех состояниях: ожидания входных ресурсов, преобразования ресурсов и блокирования. Для представления переходов его состояний используется граф состояний .
Достоинства модели (относительно требований к коалиционной модели):
– развитые средства описания информационных потоков;
– деление на активные и пассивные преобразователи ППР;
– модель позволяет работать с онтологиями предметной области.
Недостатки модели (относительно требований к коалиционной модели):
– отсутствие ориентации на мультиагентный подход;
– отсутствие возможности формирования коалиций;
– отсутствие встроенного механизма составления планов действий агентами;
– отсутствие встроенного механизма разрешения конфликтов.
Таким образом, рассмотренная модель не удовлетворяет ряду требований, предъявляемых к коалиционной модели МППР, специально не разработана для предметной области МППР.
Сравнение коалиционной модели с моделью открытой мультиагентной системы П.О. Скобелева
Открытая мультиагентная система (ОМАС) для поддержки процессов принятия решений на основе ПВ-сетей (сетей потребностей и возможностей) П.О. Скобелева базируется на холистическом подходе, состоящем в следующем:
- модель ОМАС декомпозируется на автономные сущности (деталь, материал, работник, станок, автомобиль и т.д.);
- каждая сущность имеет собственных агентов потребностей и возможностей;
- агенты возможностей ищут себе наиболее выгодное применение, а агенты потребностей − максимально удовлетворить свои требования;
- потребности и возможности (например, заказы и ресурсы) находятся в постоянном поиске соответствия (матчинга), обусловленного заданными индивидуальными критериями для каждой из сторон.
В такой открытой системе агенты потребностей и возможностей реагируют на любые изменения в системе, разрывая имеющиеся и устанавливая новые связи. МСППР рассматривается как система, состоящая из агентов возможностей и потребностей, соревнующихся или кооперирующихся между собой, в зависимости от ситуации, с целью выполнения поставленной задачи. Главной особенностью подхода (относительно предлагаемой авторами статьи коалиционной модели) является самоорганизация заказов и ресурсов. Под самоорганизацией при этом понимается возможность системы автономно устанавливать новые связи между компонентами и разрывать существующие.
Порождающей ПВ-сетью называется множество N вида:
N = {A, R, P, G},
где А − множество агентов потребностей и возможностей для заданной предметной области; R − множество возможных отношений между агентами потребностей и возможностей; Р − множество правил принятия решений и установления (разрыва) связей; G − множество целей, заданных агентам.
Архитектура ОМАС для построения ПВ-сетей состоит из базы знаний предметной области, включающей набор онтологий деятельности; сцены текущего виртуального мира; исполняющей системы; библиотеки расширений и интерфейсной системы.
Достоинства модели (относительно требований к коалиционной модели):
– простота реализации мультиагентной модели, позволившей унифицировать агентов потребностей и возможностей;
– непрерывный процесс принятия и пересмотра решений агентами позволяет системе гибко реагировать на любые события и изменения;
– агенты в модели обладают способностью самоорганизации;
– модель позволяет работать с онтологиями предметной области.
Недостатки модели (относительно требований к коалиционной модели):
– каждый ресурс и каждый заказ имеет собственных агентов, что порождает большое количество агентов, при этом любое событие в системе порождает многочисленные переговоры агентов, а также разрыв существующих связей и установление новых (такое нестабильное поведение модели требует значительное количество вычислительных ресурсов);
– отсутствие возможности формирования коалиций.
Таким образом, рассмотренная модель не удовлетворяет ряду требований, предъявляемых к коалиционной модели МППР, специально не разработана для предметной области МППР.
Сравнение коалиционной модели с моделью Д.Ю. Бугайченко
Одной из моделей, позволяющих описывать МППР, является модель Д.Ю. Бугайченко. Для описания агента в модели предложена следующая архитектура. Внешняя среда агента описывается с помощью множества S-состояний среды. Возможные действия агента описываются с помощью множества А-действий. Таким образом, агента можно представить в виде функции: S → A. Выбор конкретного действия из возможных агент осуществляет на основании текущего состояния внешней среды, а также истории, описывающей предыдущие состояния. При этом действия агента могут влиять на окружающую среду, но не контролировать ее полностью. Взаимодействие агента и внешней среды можно представлять с помощью истории (history):
h: so(a0)→s1(a1)→s2(a2)→… ,
где s0 – начальное состояние внешней среды; ai – i-е действие, выбранное агентом; si – состояние внешней среды после осуществления агентом (i-1)-го действия.
Для описания агента используется модель восприятия окружающей среды. Для этого введено множество P возможных восприятий и функция see: S → P, описывающие, каким образом определенные состояния среды воспринимаются агентом. В этом случае агент описывается с помощью функции action: P* → A, т.е. действие агента определяется текущим восприятием состояния внешней среды, а также множеством предыдущих восприятий.
Еще одной модификацией архитектуры Д.Ю. Бугайченко является агент с состоянием. Такой агент содержит внутренние структуры данных, которые он модифицирует в зависимости от восприятия текущего состояния внешней среды, и на основе полученных результатов выбирает действие. Для формализации этого процесса введено множество I внутренних состояний агента и функция refine: I × P → I, отвечающая за обновление внутреннего состояния в соответствии с текущим восприятием среды. Агент в этом случае описывается с помощью функции action: I → A, т. е. действие будет выбираться на основе текущего внутреннего состояния.
Описанная выше архитектура обладает одним существенным недостатком: определенный таким образом агент не получает информации о совершенных им самим действиях, что резко ограничивает его возможности в накоплении опыта и анализе потенциальных последствий действий. Можно считать, что информация о действиях агента является частью информации об окружающей среде, но такой подход не является наглядным и интуитивно понятным. Д.Ю. Бугайченко предложено включение информации о совершаемых действиях явно во входные данные функции выбора действия action: (P × A)* → A. В таком виде агент явно получает информацию обо всей истории взаимодействия с окружающей средой, а не только о последовательности состояний, в которые окружающая среда переходила.
Достоинства модели (относительно требований к коалиционной модели):
– детальное описание агентов, его целей, базы знаний;
– использование модели агента с состоянием, позволяющим основывать выбор действия не на последовательности входных данных, а на одном конкретном элементе состояния;
– ведение истории действий агента.
Недостатки модели (относительно требований к коалиционной модели):
– модель является слишком общей и требует детальной проработки при описании сложных МППР;
– отсутствие возможности формирования коалиций;
– отсутствие встроенного механизма составления планов действий агентами;
– отсутствие встроенного механизма разрешения конфликтов.
Таким образом, рассмотренная модель не удовлетворяет ряду требований, предъявляемых к коалиционной модели МППР, специально не разработана для предметной области МППР.
Коалиционная модель МППР разработана для предметной области ППР и имеет ряд отличительных особенностей, определяющих нишу ее адекватного применения: 1) ориентация на моделирование МППР;
2) наличие возможности описания гибридных моделей агентов;
3) наличие механизма формирования коалиций;
4) наличие механизма описания мультиагентных систем;
5) наличие аппарата взаимодействий агентов и коалиций, включающего язык, разработанный на основе стандарта взаимодействия агентов для проблемной области МППР;
6) наличие механизма разрешения конфликтов между агентами, основанного на использовании стратегий взаимодействий и организации аукционов;
7) наличие механизма составления планов действий для агентов и коалиций.
Разработанная коалиционная модель мультиагентного процесса преобразования ресурсов может быть применена для решения задач планирования и управления процессами производства на промышленных предприятиях.
--Сизов Роман (обсуждение) 22:37, 5 апреля 2016 (MSK)
[править] Simplex3: о системе имитационного моделирования
Simplex3 – универсальная имитационная система, разработанная в университетах Нюрнберг-Эрланген и Пассау (Германия), включает в себя полную среду экспериментирования и собственный объектно-ориентированный язык Simplex–MDL компактного описания системно-динамических и дискретно-событийных моделей, систем массового обслуживания, ситуационных и транспортных моделей в виде базисных и мобильных компонентов, их взаимосвязей и динамики поведения, временных и условных событий, приоритетов и процедур.
Язык моделирования Simplex–MDL содержит элементы логического программирования; расширяет объектно-ориентированный подход с помощью дополнительных механизмов связи между компонентами; делает возможным иерархическое структурирование моделей и пошаговую разработку модели, быстро собираемую из прототипов. Главным достоинством языка Simplex–MDL является простота описания моделей сложных объектов в форме, близкой к естественным параметрическим описаниям текущего состояния, сенсорных связей с другими объектами и динамики изменения состояния с помощью известных математических средств и дискретно-событийного описания.
Система Simplex3, созданная в академической среде, не предназначена для коммерческого использования, не требует больших материальных затрат и глубоких профессиональных навыков программирования на языках высокого уровня, что существенно облегчает процесс индивидуального обучения искусству моделирования и имитации в учебных заведениях и научных исследованиях в любой сфере деятельности.
Simplex3 является эффективным и легко осваиваемым инструментарием реализации агентных технологий и мультиагентного имитационного моделирования больших и сложных систем любой физической, производственной, социальной и биологической природы с созданием моделей интеллектуальных агентов с алгоритмами принятия решений и искусственного интеллекта.
Достоинствами системы является также ее многоплатформенность, инсталляция на платформе Windows через Cygwin с возможностью работы в Unix-системах, возможность подключения внешних модулей на языке C++ и возможность включения интерактивных операторов любой сложности в процесс моделирования.
Астахова Юлия (обсуждение) 23:07, 5 апреля 2016 (MSK)
Мультиагентные системы в логистике и е-коммерции. Всемирная экономика характеризуется частой сменой спроса на ресурсы, что оказывает определенное давление на производителей, которые поставляют свои товары в разные части света. Закупка мест в грузовом самолете, наем автотранспорта, аренда складских помещений, мониторинг потоков запчастей и оборудования и своевременная доставка " деловые операции, еще более трудно осуществимые теперь, чем когда-либо. Даже изнутри процесса, в рамках предприятия, логистика становится кошмаром из-за того, что покупатели часто пользуются своим правом передумать насчет параметров и характеристик своих покупок. Современные системы логистики централизованы и оптимизированы под поставку товаров "на поток?, в стабильной ситуации, следовательно, слишком негибки чтобы справиться со сложными, постоянно меняющимися внешним и внутренним потоками материалов. Производители машин в настоящее время ежегодно теряют миллионы долларов из-за негибкости своих централизованных систем материально-технического снабжения. Первая разработка компании "МАГЕНТА" в области мультиагентной логистики органично связана с е-коммерцией и будет описана далее на примере ее использования в автомобильном бизнесе - торговле, управлении системой распределения и снабжения. Используя стандартные способы предсказания спроса, производитель машин планирует производство ряда автомобилей, каждый из которых обладает набором возможного оборудования. Это - Запланированные машины. Дилеры (или, напрямую, покупатели) подают заявки на машины, указывая модель и параметры. Это - Заказанные машины. Каждая Запланированная машина также уже расписана, и агент обязан найти соответствующую Заказанную машину. Агенты взаимодействуют и легко находят подходящую пару машин. Запланированные и Заказанные машины, не нашедшие пару, уходят на второй раунд переговоров, которые, возможно, будут включать предложения о скидках или дополнительной плате для облегчения поиска подходящей пары. Современная практика разрешает покупателям изменять спецификацию заказанного автомобиля даже после того, как заказ был запущен в производство. Агент, занимающийся такой машиной, должен позаботиться, чтобы изменения были приняты во внимание, и внутренние производственные процессы были соответственно модифицированы. Такой же процесс согласования купленных машин и средств для их транспортировки должен происходить в Портале 2, как только процесс купли-продажи в Портале 1 завершен. В Портале 3 агенты должны соотносить машины и соответствующие детали и организовывать распределение деталей для конвейеров и цехов сборки машин. Основой системы "МАГЕНТА", осуществляющей согласование спроса и предложения, является команда агентов. Агенты содержатся в Базе Агентов, ожидая приписки к определенному заказу на ресурс/спрос или, другой вариант, только программные гены агентов хранятся, и они сами себя создают на базе возможных генов в момент, когда необходимы их услуги. Каждый агент знаком со своим предназначением и способен планировать собственное поведение с целью достижения его выполнения.
Мультиагентная логистика второго поколения. В будущем для того, чтобы справиться со стремительными изменениями в спросе и предложении, возможности транспортировки будут рассматриваться как предмет потребления. Поставщики деталей и транспортных услуг будут торговать опционами и заключать фьючерсные сделки. Краткая версия сценария для интеллектуальных систем материально-технического снабжения второго поколения, разработанный компанией "МАГЕНТА", предлагается далее. Основным нововведением в нем является замена штрихового кода на электронные знаки, каждый из которых содержит агента. После получения опционов на транспортировку, поставщик должен послать поток Интеллектуальных Посылок (посылок с интеллектуальными электронными знаками, каждый из которых содержит простого интеллектуального агента, встроенного в чип, имплантированный в упаковочный материал) в Центр Всемирной сети логистики (GLN). Каждый посланный агент имеет знания о месте своего назначения, ожидаемом времени прибытия, пути следования, условиях складирования и эксплуатации, весе и размерах. Каждый Центр GLN (склады, транспорт) будет иметь своих собственных агентов, способных общаться с вверенными им интеллектуальными агентами. При прохождении через GLN Посылки будут регулярно обновляться через Интернет в соответствии с изменением места их назначения и времени прибытия. Как только становится известно новое место назначения, агенты в Посылках и агенты Центров GLN начинают вести переговоры по поводу новых путей следования по Сети - индивидуально для каждой Посылки. В случае необходимости агенты в Посылках будут покупать новые транспортные опционы для продолжения своего путешествия. Агенты будут способны сделать это без обращения к поставщикам Посылок. Этот сценарий демонстрирует развитие изначально распределенной, самоорганизующейся системы логистики, обеспечивающей снижение временных и материальных транспортных расходов. Плюс к этому, она обеспечит экологически чистое решение проблемы урона, нанесенного окружающей среде нерациональным передвижением товаров вокруг земного шара. Прототип такой системы будет разработан уже через год. Последующее ее развитие будет идти по нарастающей. Необходимые пространство для складирования и средства транспортировки могут быть добавлены в сеть когда будет нужно и в необходимом количестве. После этого можно будет проектировать GLN для дальнейшего роста и развития, как это было с сетью Интернет.
--Шентерова Алена (обсуждение)
Мультиагентная модель поведения толпы Современные тенденции в обеспечении безопасности социальных систем, требуют решения целого ряда актуальных проблем, разрешение которых позволило бы повысить уровень безопасности общества. Реалии проведения массовых мероприятий показывают, что подобные акции зачастую являются главной мишенью для различных экстремистки, настроенных групп людей. Поэтому на первый план выходят проблемы их безопасного проведения. Планирование мероприятий подобного класса требует учета большого количества факторов. Одним из них является территория их проведения. Опыт показывает, что неудачное расположение строительных и других объектов в местах скопления людей, является одной из главных причин возникновения ситуаций подобных давке, влекущих за собой состояние паники и огромное количество жертв. В тоже время эффективное расположение спец. предметов (заградительные щиты, поручни, и т.д.) на имеющейся территории может существенно снизить вероятность возникновения ситуаций, прямо или косвенно угрожающих жизни людей. Для определения мест установки подобных заграждений необходимую помощь может оказать система моделирования поведения коллективов людей. Работы в области искусственного интеллекта, а также современные подходы к психологическому осмыслению взаимодействия людей позволяют осуществить попытку спроецировать толпу, как социальное образование, в техническую плоскость мультиагентных систем. Рассматривая поведение человека в социальной среде, можно сделать предположение, что поведение отдельного индивидуума в большей степени зависит от ситуации, создаваемой ему соседями, чем от личностных побуждений самого субъекта. Таким образом, поведение коллектива в целом складывается из попыток отдельных людей реализовать свои желания. Анализируя поведение толпы, как социального образования для абсолютного большинства субъектов наибольший приоритет имеет желание переместиться, точнее, сделать шаг, определенный его текущей целью. Поэтому поведение толпы в первом приближении может определяться механическим взаимодействием внутри коллектива. Природа подобных контактов может быть прямой или опосредованной, ибо два человека могут взаимодействовать между собой и производить прямое физическое воздействие, находясь в непосредственной близости, а также влиять друг на друга через других участников, подталкивая их к тем или иным шагам. Для идентификации своих последующих шагов агента модель должна учесть физиологическую неоднородность коллектива. Каждому отдельному человеку свойственен предел физических возможностей, определенный в каждом отдельном случае индивидуально. С другой стороны, вероятность встретить в толпе человека, к примеру, массой m, может быть установлена статистическими методами. В первом приближении она может быть распределена согласно закону Гаусса, с центром в точке статистически среднего веса в исследуемом коллективе. Согласно данному подходу могут быть введены другие физические величины и законы их изменения. Система получает определенную степень гибкости относительно механической части проблемы. Добавляя в расчетную часть восприятие психологических компонентов, мы конструируем модель поведения толпы, имеющую высокую степень адекватности реальной. Качество воспроизведения моделью свойств толпы возрастает пропорционально количеству учтенных в ходе моделирования сторон взаимодействия лиц ее составляющих. Таким образом, разрабатывая модель поведения толпы, получаем мультиагентную систему, в которой на «выходе» каждого агента имеем вектор, определяющий его физическое и эмоциональное состояние. Интерпретация этих данных проводится каждым агентом индивидуально за счет уникальности его параметров. При их генерации учитываются физиологические и психологические особенности индивида. Если для нахождения механических параметров агента зачастую достаточно определить вес моделируемого субъекта (остальные параметры можно вывести из классических законов Ньютона), то для определения психического состояния можно ввести понятие «энергия» агента. Энергией агента назовем величину, определяющую близость субъекта к состоянию паники. Каждый агент имеет порог, по достижении которого он переходит в состояние паники. Состояние паники характеризуется желанием агента как можно скорее покинуть территорию, прямо или косвенно угрожающую его «здоровью», т.е. максимально быстро достичь безопасного местоположения. Определение таких мест каждый агент проводит самостоятельно. В общем случае для локализации такого положения агент ищет точку, максимально удаленную от паникующих соседей. Чем больше превышение энергией порога, тем большее расстояние требуется агенту для «успокоения». Энергия агента динамически изменяется в процессе моделирования, так как является составной частью психики агента. Повышенное эмоциональное состояние соседних субъектов «отрицательно» сказывается на уровне энергии самого агента. Чем больше количество паникующих субъектов вокруг, тем ближе величина его энергии к порогу. Сам факт перехода соседним агентом порогового состояния оказывает дополнительное психологическое воздействие. Просуммировав все перечисленные моменты можно записать алгоритм функционирования отдельного агента системы:
1. Определить координаты цели своего перемещения. Для агента находящегося в состоянии паники целью перемещения будет точка, удаленная от толпы на расстояние, определенное энергией агента. С каждым шагом, направленным на отделение агента от толпы, величина энергии удаляется от значения порога, т.е. перемещение в клетку с меньшим количеством агентов вызывает уменьшение начальной энергии агента E0. Для агента, находящегося в нормальном состоянии цель совпадает с общей направленностью движения в случае моделирования проведения демонстраций и т.п., либо случайно выбранное направление в случае моделирования поведения людей в универмагах. Если какая-либо ячейка недоступна, то на ее месте фиксируется непроходимая клетка. После определения цели агент с помощью одного из методов трассировки находит к ней путь. В ходе проектирования модели использовался волновой алгоритм трассировки.
2. Определить направление следующего шага. После того как цель определена, необходимо соотнести свой следующий шаг с общим положением окружения. Каждый соседний агент имеет свое приоритетное направление, поэтому возможность перемещения будет зависеть от физических параметров человека и состояния психической энергии. Таким образом, на данном этапе агент производит разворачивание суммарного образа, создаваемого всей совокупностью соседних субъектов, и определяет на его основе направление следующего шага. Если перемещение в направлении выбранного целью шага невозможно, например, в этом направлении на данном шаге образовалась пробка, то выбирается следующая цель. Если целей нет, то наращивается значение энергии (растет беспокойство) и агент остается на месте.
3. Скорректировать текущее значение энергии. Необходимо определить общий энергетический фон и количество соседей, перешагнувших свой порог и сравнить с показателями на предыдущем шаге. Энергия агента изменяется исходя из следующего выражения: E f E f m kE Rn = 1 ( 0 ) + 2 ( ) + p − ,где f1 – восприятие энергетического фона; Е0 – начальная энергия агента; n – количество агентов в ячейке; m – количество соседей переступивших порог энергии; f2 - восприятие агентом факта перехода соседей в состояние паники; R – сопротивление клетки; Ер – прирост энергии при ошибке в нахождении пути; k – количество перебранных целей в ходе определения пути.
4. Сделать шаг. Следующим шагом в построении модели является формирование среды обитания агентов. В зависимости от выбранного шаблона соседства для отображения территории может использоваться матрица (4- или 8- линковый шаблон), либо более сложная структура. В случае использования матрицы каждой ее клетке однозначно сопоставлен элемент моделируемой площади, который имеет некоторый набор свойств. Для системы минимум необходимы следующие параметры ячейки: ёмкость С; сопротивление R. Емкость С есть величина, характеризующая максимальное количество агентов единовременно находящихся на единице площади. Значение сопротивления R определяет минимальный уровень психофизических параметров, оказываемый одним агентом своему соседу. Величина Rn в формуле определяет минимальный уровень энергии агента необходимый для продвижения агента в данную ячейку (чем больше плотность людей в толпе, тем более сильный барьер представляет собой клетка для агента). Величина шага агента определяется значением его энергии в соответствии со следующей формулой: dS = 0.01* E ,где E ∉[0,100] - энергия агента. Таким образом, максимальное расстояние, которое может преодолеть агент за один шаг равно 1 ячейке. Это сопоставимо с площадью одной клетки в 1 м2. Чем ближе уровень энергии агента к критическому уровню и больше его физические возможности, тем более высокий барьер агент может преодолеть. Каждое новое появление агента в ячейке отображается увеличением ее сопротивления, и наоборот, выход агента из нее сопровождается уменьшением сопротивления. Территория может иметь вид:.
Если сопротивление ячейки нормировать, то значение 0 и 1 будут означать наибольшую и наименьшую вероятность преодоления агентом ячейки соответственно. Следовательно, нахождения на территории значений в промежутке [0,1] обозначат препятствия: окна, столы, стулья и т.д. Вернувшись к первоначальной задаче, имеем мультиагентную систему, воспроизводящую модель поведения коллектива людей и систему моделирования среды их обитания. Для определения мест установки заградительных барьеров представим среду обитания в виде матрицы, в клетках которой расположены значения от нуля до единицы, дублирующие матрицу территории. Представим матрицу в виде строки и получим вектор M={a1,а2, …, аn}, где аi - сопротивляемости соответствующих элементарных площадей территории. Зафиксировав ячейки, отображающие статические препятствия, например, стены, можно моделировать поведение людей на исследуемом объекте. На основании этого можно построить генетический алгоритм нахождения оптимальных мест расположения препятствий. Задав общую цель для всех агентов (например, ячейки за пределами помещения) и целевую функцию в виде времени (или шагов моделирования), за которое все агенты покидают помещение, можно оптимизировать матрицу сопротивлений согласно простому генетическому алгоритму. Кроме времени, в целевой функции может фигурировать минимальная площадь, занимаемая препятствиями. В качестве решения получаем матрицу, в которой указаны координаты мест установки препятствий. Об их виде можно судить по значению коэффициента сопротивления, чем он больше, тем более серьезное оборудование требуется. --Александра Ванюхина (обсуждение) 00:05, 6 апреля 2016 (MSK)
Координация поведения агентов в мультиагентной системе
Наиболее известными моделями координации поведения агентов являются: теоретико-игровые модели, модели коллективного поведения автоматов, модели планирования коллективного поведения, модели на основе BDI-архитектур (Belief – Desire – Intention), модели координации поведения на основе конкуренции.
Теоретико-игровые модели. Предметом теории игр являются задачи выбора решений в условиях неопределенности и конфликта. Наличие конфликта предполагает существование как минимум двух участников, которых называют игроками. Множество решений, возможных для выбора каждым игроком, называется стратегией. Равновесными точками игры (оптимальными решениями) называют такие состояния, когда ни одному из игроков невыгодно менять свою позицию. Понятие равновесия оказалось весьма полезным в теории MAC, поскольку механизм поиска равновесных ситуаций может использоваться как средство самоорганизации коллективного поведения агентов. Следствием подобной интерпретации является подход, в котором необходимые атрибуты коллективного поведения агентов обеспечиваются путем конструирования правил игры. Кроме того, на основе развития теории игр в области MAC предпринимаются попытки построения эффективных, устойчивых, полностью распределенных протоколов переговоров, направленных на координацию коллективного поведения агентов.
Множество возможных ситуаций выбора поведения пары агентов классифицируется следующим образом.
1. Симметричная кооперация, когда существует непустое множество стратегий (переговорное множество), при использовании которых оба агента достигают своих целей и получают больший эффект, чем в ситуациях, когда они действуют поодиночке.
2. Симметричный компромисс, когда достижение цели в одиночку более выгодно для каждого агента, однако невозможно в присутствии другого агента.
3. Несимметричная кооперация или несимметричный компромисс_– один из агентов может самостоятельно достичь своей цели в присутствии другого агента, а другой – только засчет кооперации с первым.
4. Конфликт – переговорное множество пусто, т.е. не существует стратегий, обеспечивающих достижение целей обоих агентов.
Теоретико-игровые модели позволяют для всех перечисленных случаев сконструировать наборы правил переговоров, следуя которым агенты придут к некоторому соглашению, отвечающему состоянию равновесия. Это достигается засчет использования множества дополнительных предположений и специальных приемов. Например, кроме стоимости цели в рассмотрение вводится понятие ценности цели, а в качестве одной из возможных стратегий может выступать стратегия манипулирования информацией о ценности целей (т.е. агенты могут сообщать друг другу заведомо ложные значения). При этом «нечестные» агенты могут либо увеличить свой доход, либо освободиться от части своей работы.
Модели коллективного поведения автоматов. Они основаны на идеях рандомизации, самоорганизации и полной распределенности. Модели этого типа подходят для построения протоколов переговоров в задачах, которые характеризуются большим количеством очень простых взаимодействий с неизвестными характеристиками.
Модели планирования коллективного поведения. Планирование может быть централизованным, частично централизованным или распределенным (децентрализованным). В последнем случае агенты сами принимают решения о выборе своих действий в процессе координации частных планов, всвязи с чем возникают вопросы о рациональной децентрализации, о возможности изменения целей при возникновении конфликтов, а также проблемы вычислительной сложности.
Модели на основе BDI-архитектур. В моделях этого класса применяются аксиоматические методы теории игр и логической парадигмы искусственного интеллекта. Для описания агентов используются логические средства, в том числе темпоральные и модальные логики. Акцент делается на описании интенсиональных понятий, таких, как убеждения (belief), желания (desire) и намерения (intention). Задача координации поведения агентов решается путем согласования результатов логического вывода в базах знаний отдельных агентов, полученных для текущего состояния внешней среды, в которой действуют агенты. Логический вывод осуществляется непосредственно в процессе функционирования агентов, что приводит к высокой сложности моделей, вычислительным трудностям и к проблемам, связанным с аксиоматическим описанием нетривиальных ситуаций, например, когда перед агентом возникает выбор между решением собственной задачи и выполнением обязательств по отношению к партнерам.
Модели на основе конкуренции. В моделях данного класса используется понятие аукцион в качестве механизма координации поведения агентов. Использование механизма аукциона основано на предположении о возможности явной передачи «полезности» от одного агента к другому или к агенту-аукционеру, причем эта полезность обычно имеет смысл денег.
Аукционы принято разделять на открытые и закрытые. В первом случае предлагаемые цены объявляются всем участникам. В закрытом аукционе о предлагаемых ценах знает только аукционер. Открытые аукционы различаются по способу проведения. В так называемых английских аукционах обычно задается стартовая цена, которая может увеличиваться участниками в ходе торгов. Побеждает тот, кто даст максимальную цену. Голландский аукцион начинается с верхней цены, которая постепенно снижается. Победителем считается тот, кто дал наибольшую текущую цену. Закрытые аукционы разделяют на аукционы первой и второй цены. В аукционах первой цены побеждает тот, кто предложил самую высокую цену, известную только аукционеру. В аукционах второй цены победитель определяется таким же способом, но платит за товар не свою цену, а вторую по величине. Теоретически доказано, что все разновидности аукционов эквивалентны для аукционера, однако практика показывает иное. Например, если участники аукциона не склонны к риску, то аукционер стимулирует повышение цены продажи при проведении голландского аукциона первой цены. Существуют варианты «групповых» аукционов, когда один или несколько участников представляют интересы группы, и в случае выигрыша проводится аукцион внутри группы. При этом на внутреннем аукционе товар продается по более высокой цене по сравнению с ценой внешнего аукциона. Полученная разница делится между участниками группы.
Сам по себе механизм аукциона не затрагивает способов принятия решений участниками. Решения могут приниматься на основе некоторой модели рассуждений, которая может использовать различные типы знаний, доступных агентам, и разнообразные способы их обработки.
Аукцион всегда должен заканчиваться. Для этого в стратегии его проведения должны быть заложены средства для разрешения возможных конфликтов (например, при наличии нескольких победителей). Одним из самых простых способов разрешения конфликтов является рандомизация, когда применяется случайный механизм выбора.
--Суханова Елена (обсуждение) 00:10, 6 апреля 2016 (MSK)
[править] Управление образовательными системами с использованием мультиагентных технологий
Образовательные системы представляют собой социальные институты, целью которых является образование человека. Как и любые системы, они имеют свою структуру, т.е. состоят из определенных элементов, которые взаимосвязаны между собой. Взаимодействие различных элементов образовательной системы или ее подсистем направлено на достижение общей для системы цели, общего положительного результата, и эта цель – обучение, воспитание и развитие личности.
Федеральный закон «Об образовании в Российской Федерации», вступающий в силу 01 сентября 2013 года, определяет три основные программы высшего профессионального образования (ВПО): бакалавриата, специалитета и магистратуры . Бакалавриат и магистратуру можно рассматривать как отдельные образовательные подсистемы, связанные между собой, в то время как специалитет является непрерывной одноуровневой подсистемой образования, в связи с чем в данной статье как образовательная подсистема не рассматривается. Сложность и изменчивость современного мира не позволяет исследовать его, а тем более управлять им с помощью традиционного, жестко организованного программного обеспечения. Поэтому одним из путей создания нового программного обеспечения, способного приблизить человека к адекватному описанию окружающего мира, является применение мультиагентных технологий (МАТ). МАТ представляют собой направление искусственного интеллекта, основанное на взаимодействии нескольких интеллектуальных агентов в распределенных системах. При этом каждый агент наделяется конкретным набором свойств в зависимости от целей разработки, решаемых задач, технологии реализации, заданных критериев. В связи с этим для решения сложной задачи необходимо создать некоторое множество агентов и организовать между ними эффективное взаимодействие, что позволит построить единую МАС.
МАТ используют для построения СППР в таких областях, как распределенное решение сложных задач, совмещенное проектирование изделий и построение виртуальных предприятий, имитационное моделирование интегрированных производственных систем и электронная торговля, организация работы коллективов роботов, распределенная разработка компьютерных программ, интеллектуальная обработка информации, в том числе семантический поиск, интеллектуальный анализ данных, адаптивное планирование. Однако для моделирования процесса отбора студентов до сих пор МАС не применялись.
Проведенный анализ эффективности стандартных математических методов показал, что наиболее перспективными для оптимизации процесса отбора студентов на магистерские программы являются следующие:
- логический анализ на основе применения булевых функций при определении профиля магистратуры без учета индивидуального уровня качества освоения образовательной программы бакалавриата для каждого выпускника;
- дискриминантный анализ, позволяющий на основе оценки индивидуальных академических достижений, а также уровня мотивации определить группу для дальнейшего обучения;
- комбинаторный анализ, позволяющий на основе данных о несформированных компетенциях бакалавра построить образовательный маршрут магистра, учитывающий освоение дисциплин, формирующих требуемые компетенции, и распределение их по семестрам.
Архитектура СППР представлена шестью агентами, базой знаний (БЗ) и базой данных (БД). Связь с системой осуществляется посредством агента-супервизора. Блок принятия решений концептуальной схемы включает агента-консультанта и агента-исполнителя. Блок анализа проблем представлен агентом-экспертом, агентом-классификатором и агентом-оптимизатором. Координация агентов в системе осуществляется на основе непрямого взаимодействия, которое соответствует распределению функциональных задач МАС.
БЗ – важный компонент МАС. Она представляет собой особую БД, разработанную для оперирования знаниями в виде функциональных связей между компетенциями магистра и бакалавра. БЗ содержит структурированную информацию, необходимую агенту-эксперту для управления отбором студентов. МАС позволяет формировать новые знания и пополнять ими БЗ, а также хранить и извлекать знания в случае необходимости. БД также является необходимым компонентом МАС. Она позволяет в структурированном виде хранить и обрабатывать динамические (информация о выпускниках-бакалаврах, ООП магистратуры и бакалавриата) и статические (перечень компетенций магистра и бакалавра согласно ФГОС ВПО) наборы данных. Работу с БД организует агент-супервизор. Агент-супервизор – интерфейсный агент, решающий задачу взаимодействия агентов МАС и связи с пользователем. Он ведет диалог с СППР, сообщая ей сведения о текущем выпускнике и получая рекомендации СППР. Кроме этого, агент-супервизор осуществляет формирование компьютерной БД с информацией о направлениях подготовки и соответствующих им компетенциях (на основании ФГОС ВПО и разработанных в вузе ООП).
Агент-эксперт – гибридный агент, в задачу которого входит определение оптимального профиля магистратуры на основе правил приема на вторую ступень вуза и ограничений, установленных вузом и стандартами в области ВПО. Данный агент вводит известные ему сведения о функциональных связях между компетенциями магистра и компетенциями бакалавра в БЗ. Агент-классификатор – гибридный агент, который осуществляет формирование шаблонных комбинаций интегрированных средних оценок уровня сформированности компетенций [3] и уровня мотивации, а также деление всех претендентов в магистратуру на две группы в зависимости от уровня их подготовки в бакалавриате. Агент-оптимизатор – гибридный агент, осуществляющий формирование образовательного маршрута магистранта на основе анализа приложения к диплому и компетентностной модели выпускника-бакалавра. Агент-консультант – гибридный агент, задачей которого является слежение за процессом приема в магистратуру, принятие решений (совместно со студентом) по выбору для выпускника-бакалавра ООП. Агент-исполнитель – гибридный агент, задачей которого является принятие решений (совместно с агентом-консультантом) по выбору образовательной программы. Данный агент является непосредственно выпускником-бакалавром.
Взаимодействие агентов в системе осуществляется следующим образом. Агент-супервизор формирует задание по определению магистерской программы для группы выпускников-бакалавров, обучавшихся по одной и той же ООП, которое в виде входного сообщения поступает агенту-эксперту. После этого агент-эксперт пополняет БЗ необходимыми записями, содержащими информацию о функциональных связях между компетенциями магистра и бакалавра (на основе логического анализа). Далее агент-эксперт на основе анализа знаний из БЗ осуществляет формирование нескольких ООП магистратуры, по которым выпускники могли бы продолжить обучение. Перечень этих образовательных программ передается агенту-консультанту. Агент-консультант, взаимодействуя с каждым выпускником по отдельности, осуществляет выбор наиболее приемлемого для студента профиля магистратуры (другими словами, выбор ООП магистратуры) и наполняет систему информацией об его академических и научно-исследовательских достижениях. После того, как получена информация обо всех претендентах в магистратуру, агент-классификатор формирует учебные группы по каждому профилю магистратуры в соответствии с уровнем «продвинутости» групп (на основе дискриминантного анализа). Далее он посылает агенту-консультанту сообщения о возможности или невозможности формирования заданных групп. В случае недобора абитуриентов в какие-либо группы выпускникам-бакалаврам предлагается изменить свой выбор в пользу другого профиля магистратуры, по которому могут быть сформированы учебные группы. Итоговые списки академических групп передаются агенту-супервизору. Для студентов, которые освоили не все компетенции бакалавра, необходимые для обучения в магистратуре, агент-оптимизатор осуществляет формирование индивидуальных образовательных маршрутов и определяет перечень дисциплин, которые им необходимо изучить, а также распределяет эти дисциплины по семестрам (на основе комбинаторного анализа).
Для оценки адекватности предложенной МАС были рассмотрены четыре сценария принятия решений по набору выпускников-бакалавров на направление подготовки магистратуры 230100.68 «Информатика и вычислительная техника»:
- с соблюдением профильности базового образования (отбор выпускников направления подготовки бакалавриата 230100 «Информатика и вычислительная техника», профиль – «Автоматизированные системы обработки информации и управления»);
- без соблюдения профильности базового образования (отбор выпускников направления подготовки бакалавриата 022000 «Экология и природопользование», профиль – «Экология»);
- с учетом мотивации к дальнейшему обучению (отбор выпускников направления подготовки 230100.62 «Информатика и вычислительная техника», а также выпускников нескольких других направлений подготовки, близким с данным, но с большим уровнем мотивации);
- с формированием образовательного маршрута (отбор выпускников любых направлений подготовки бакалавриата с учетом недостающих дисциплин и их освоения в процессе обучения в магистратуре).