Результаты исследований обучающихся в проекте Познаем мир с помощью моделей
Содержание |
Авторы и участники проекта
Красильникова Надежда Сергеевна
Участники группы "Аналитики"
Тема исследования группы
Использование графа для выбора оптимального решения
Проблемный вопрос (вопрос для исследования)
Как найти оптимальное решение?
Гипотеза исследования
Предположим, что решение задачи с помощью графа приведет к выбору оптимального решения.
Цели исследования
1) Провести анкетирование в классе на тему «Графы в нашей жизни»
2) Проанализировать теоретические сведения о графах
3) Решить задачу с помощью графа
3) Исследовать использование моделирования на графах в различных предметных дисциплинах
Результаты проведённого исследования
В результате исследования группа разработала анкету. Затем было проведено анкетирование в классе на тему «Графы в нашей жизни».
Форма для опроса Анкета группы "Аналитики"
Результаты анкетирования мы представили в виде диаграмм, на основе ответов.
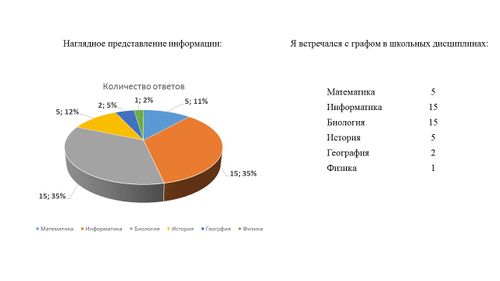
Результаты 1 вопроса группы "Аналитики"
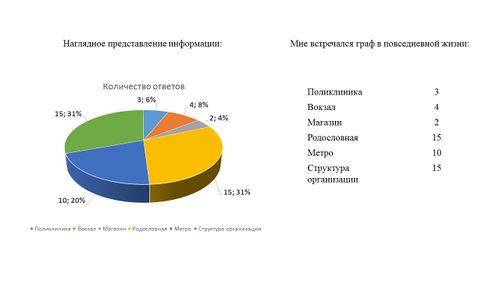
Результаты 2 вопроса группы "Аналитики"
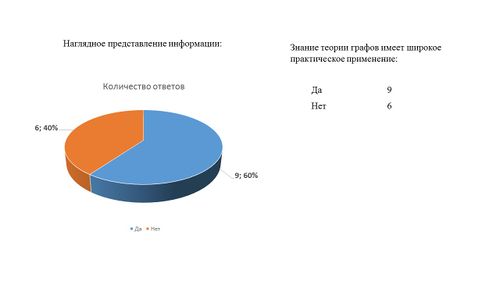
Результаты 3 вопроса группы "Аналитики"
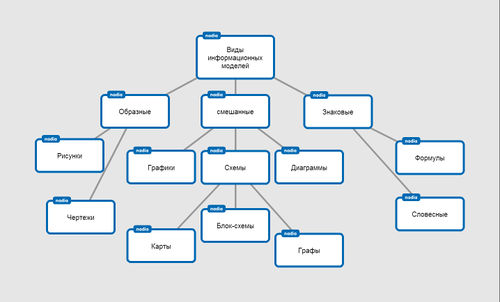
Далее мы решили построить карту знаний "Виды информационных моделей по способу представления" при помощи сервиса popplet.com:
Вывод
В результате нашего исследования в рамках данного проекта мы выяснили следующее:
1. Всем известно, что слово «граф» означает дворянский титул, например граф Лев Николаевич Толстой. А вот в математике графом называют множество точек, изображенных на плоскости, некоторые из которых соединены линиями. Точки именуются вершинами графа, а отрезки – ребрами.
2. Задачи решаемые с помощью графов обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления. Язык графов прост, понятен и нагляден. Графовые задачи допускают изложение в занимательной, игровой форме. С другой стороны, для их решения не требуется глубоких знаний, следует применять смекалку.
3. Основы теории графов как математической науки заложил в 1736 году Леонард Эйлер, рас-сматривая задачу о кенигсбергских мостах. Бывший Кенигсберг (ныне Калининград) распо-ложен на реке Прегель. В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены. Кенигсбергцы рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз и вернуться к тому месту, откуда началась прогулка. Многие горожане за-интересовались этой задачей, однако придумать решение никто не смог. Этот вопрос при-влек внимание ученых разных стран. Разрешить проблему удалось известному математику Леонардо Эйлеру. Причем, он не только решил эту конкретную задачу, но придумал общий метод решения подобных задач. Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты « вытянул» в линии.
4. Теория графов в настоящее время является интенсивно развивающимся разделом математики и информатики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации: коммуникационные сети, схемы электрических и электронных приборов, химические молекулы, отношения между людьми, всевозможные транспортные схемы и многое-многое другое. Сетевые графики используют не только строители, но и конструкторы машин с большим количеством узлов и деталей, диспетчеры железных дорог и многие другие специалисты. Все это очень важно для нормального функционирования общественной жизни. Именно этот фактор определяет актуальность более подробного изучения графов. Опрос «Графы в нашей жизни», который наша группа провела в классе, полностью подтверждает этот вывод.
5. В настоящем проекте рассмотрены графы, области их применения. Также приводятся задачи, решенные с помощью теории графов. Графы достаточно широко применяются в математике, технике, экономике, управлении. Знание основ теории графов необходимо в различных областях, начиная с химических мо-лекул и кончая управлением производством и бизнесом (например, сетевой график строи-тельства). Еще раз мы убедились в том, что теория графов имеет широкое практическое применение. Теория графов находится сейчас в самом расцвете.
Полезные ресурсы
Статья в Википедии "Открытая система"
Статья в Википедии "Систематизация"