О чем может рассказать график функций?

Автор проекта

Учащиеся 9 класса

Тема исследования группы

Исследование функции

Цели исследования

• рассмотреть различные способы задания функции;
• выяснить в чем преимущества и недостатки различных способов задания функции?
• показать как можно исследовать функцию?

Результаты проведённого исследования

Определение функции: Функцией у=f(x) называется зависимость, по которой каждому значению независимой переменной ставится в соответствие единственное значение другой зависимой переменной. Если прямая параллельная оси ординат пересекает график только в одной точке, то это график функции. Переменная, значение которой выбирается произвольно, называется независимой переменной (аргументом), а переменная, которая определяется по некоторому правилу, называют зависимой переменной (функцией или значение аргумента). Например y=3x+4 x – независимая переменная, y – зависимая переменная у=f(x) x – независимая переменная, y – зависимая переменная g=f(t) t – независимая переменная, g – зависимая переменная

График функции - множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции

Существуют различные способы задания функций

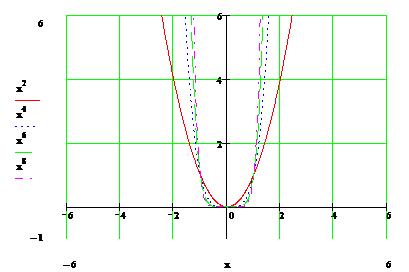
• с помощью формулы

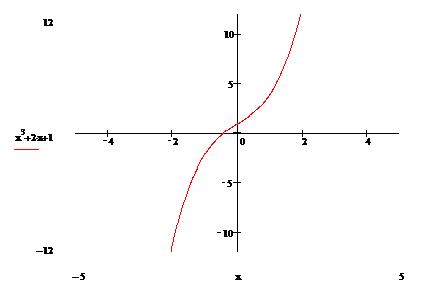
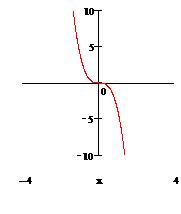
y=x³, y=x²+4x-4 y=x+12

• табличный

x	5	3	4	6
y	3	4	3	1

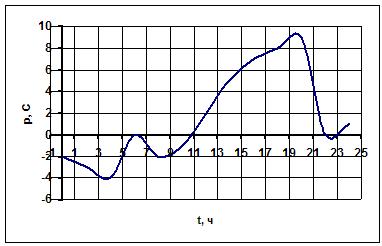
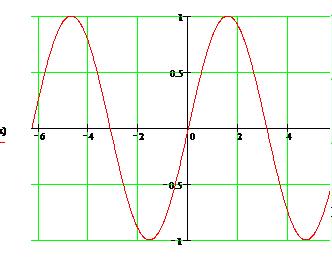
• графический

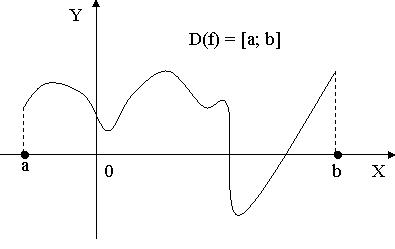
Область определения функции – это те значения, которые может принимать независимая переменная (х). Обозначение: D(f) или D(y)

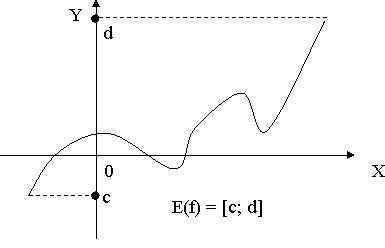
Область значения функции – это те значения, которые может принимать зависимая переменная (y). Обозначение: E(f) или E(y).

Функция называется числовой, если область определения(D(f)) и область значения(E(f)) – числовые промежутки.

Функция у=f(x) называется чётной функцией , если выполняются два условия:

• Область определения функции – симметричное множество относительно числа 0.

(Симметричным множеством чисел называется множество, где с каждым числом х, присутствует и число –х.)

• Выполняется равенство f (-x) = f (x)

График чётной функции расположен симметрично относительно оси ординат.

Функция у=f(x) называется нечётной функцией , если выполняются два условия:

• Область определения функции – симметричное множество относительно числа 0.
• Выполняется равенство f(-x) = -f(x)

График нечётной функции расположен симметрично относительно начала координат.

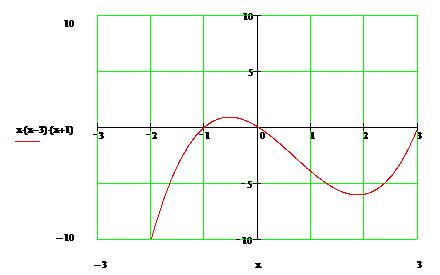
Нули функции – это те значения переменной, при которых значения функции равны нулю. Для того, чтобы найти нули функции y=f(x) необходимо решить уравнение f(x)=0. Нули функции так же называют корнями функции. Функция может иметь несколько нулей. Например, функция y=x(x+1)(x-3) x(x+1)(x-3)=0 имеет три нуля: x=0, x=-1, x=3. Графически нуль функции – это абсцисса точки пересечения графика функции с осью абсцисс. На рисунке представлен график функции с нулями: x=-1, x=3 и x=0.

Промежутки знакопостоянства функции – это промежутки, на которых функция сохраняет (не меняет) знак(то есть остаётся положительной y>0 или отрицательной y<0). О промежутках знакопостоянства функции легко судить по графику y>0(часть графика расположена выше оси абсцисс ОХ), y<0(часть графика расположена ниже оси абсцисс ОУ). Определим промежутки знакопостоянства функции для функции y= (x+1)(x-3)

y>0 на промежутке [-1;0]

y<0 на промежутках [-2;-1]и[0;2]

Функция y=f(x) называется возрастающей на промежутке X, если большему значению аргумента соответствует большее значение функции.

Функция y=f(x) называется убывающей на промежутке X, если большему значению аргумента соответствует меньшее значение функции.

Схема элементарного исследования функции

1. Указывается область определения (Д(у)=…) и область значения (Е(у)=…)
2. Указывается функция является чётной, нечетной или ни чётной ни нечётной
3. Определяются нули функции (графически – точки пересечения с осью Х)
4. Указываются промежутки знакопостоянства функции
5. Указываются промежутки возрастания и убывания функции.

Вывод

Рассмотрев различные способы задания функции, мы сделали выводы:

Три способа задания функции связаны между собой. Преимущества табличного способа – это наглядность. Задание функции формулой позволяет находить по любому значению аргумента, соответствующее значение функции и решать обратную задачу.

С помощью графика можно определить область определения, область значения, нули функции, четность функции, промежутки знакопотоянства, возрастающая функция или убывающая.