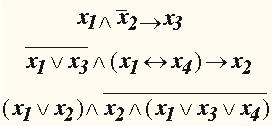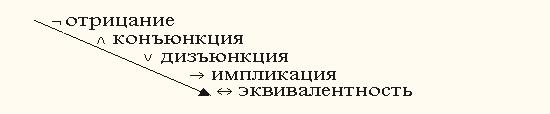Вики-учебник для подготовки к ЕГЭ/Раздел Информатика/Основы логики/Логические выражения и их преобразование
Содержание |
Содержательное обобщение изученного материала
Элементарные высказывания
Основным объектом изучения математической логики являются элементарные высказывания. Под термином "высказывание" мы будем понимать повествовательное предложение. При этом нас будет интересовать не построение: подлежащее - сказуемое - дополнение, а характерные свойства рассматриваемых образований: являются они истинными или ложными. Высказывания отличаются от других языковых образований тем, что мы можем присвоить им определенное значение истинности - "истина", если они истинны, значение "ложь", если они ложны. При этом мы исходим из "принципа исключенного третьего", или "третьего не дано", который состоит в том, что каждое высказывание или истинно, или ложно, и других возможностей нет. Ситуация, когда ни истинно, ни ложно, была бы и в обычном смысле неразрешимой. Этот принцип называют принципом двузначности. Все научные знания (законы и явления физики, химии и биологии, математические теоремы и т.д.), события повседневной жизни, ситуации, возникающие в процессах управления, формулируются в виде высказываний.
Примерами указанных высказываний являются:
"36 делится на 6", "Москва - столица России".
Все они имеют значение истинности "истина".
Следующие высказывания имеют значение истинности "ложь":
"Мышь больше слона",
"Молодые лошади называются щенятами",
"6 больше 8".
Повелительные ("Войдите, пожалуйста!"), вопросительные ("Знаешь ли ты информатику?") и бессмысленные предложения не являются высказываниями.
Если логика имеет дело со смыслом высказываний, то в алгебре логики работают с формулами.
Любое элементарное высказывание обозначается малой буквой латинского алфавита, совершенно так же, как в элементарной алгебре обозначаются величины, когда мы абстрагируемся от того, какие именно предметы изучаются, нас интересует только их количество и соотношение между ними. Поскольку высказывание может принимать одно из двух значений, то говорят о "переменных высказываниях". Это означает, что рассматривается не только конкретно определенное высказывание хi , но также некоторая логическая переменная х i , которую можно использовать для обозначения произвольного высказывания. Замещение переменной конкретным высказыванием означает предоставления одного из значений "истина" или "ложь".
Итак, в алгебре логики в каждом высказывании мы будем отвлекаться от всех особенностей высказывания, кроме одного - истинно оно или ложно. Истинное высказывание условно обозначается единицей (если x1 - высказывание " 36 делится на 6", то x1 = 1), а ложное - нулем (если x2 - высказывание "мышь больше слона", то x2 = 0).
Таким образом, диапазон изменения переменного - xi в алгебре логики существенно меньше, чем изменение переменного в элементарной алгебре: оно принимает только одно из двух значений - или 1, или 0.
Логические операции
Из элементарных высказываний с помощью логических связок " и", "или", "не", "если : то" и других (логических операций) строятся сложные высказывания - формулы (или функции ) алгебры логики.
В алгебре логики основными (элементарными) операциями являются:
- отрицание,
- логическое сложение (дизъюнкция),
- логическое умножение (конъюнкция),
- импликация,
- эквивалентность.
Способы построения новых высказываний из заданных с помощью логических связок, их преобразования и установления истинности изучаются в логике высказываний с помощью алгебраических методов.
Основные соотношения
| 0 •0 = 0, | 0 \/ 0 = 0, | |
|---|---|---|
| 0 • 1 = 0, | 0 \/ 1 = 0, | |
| 1 • 0 = 0, | 1 \/ 0 = 0, | |
| 1 • 1 = 1, | 1 \/ 1 = 1, | |
Основные тождества
| X • 0 = 0, | X \/ 0 = X, | |
|---|---|---|
| X • 1 = X, | X \/ 1 = 1, | |
| |
|
|
| X • X •...• X = X , | X \/ X \/...\/ X = X, | |
Сложное высказывание
В логических задачах исходными данными являются суждения, подчас неожиданные и нередко весьма запутанные. Высказывания и связи между ними бывают иногда столь противоречивыми, что такие "твердые орешки" не под силу "раскусить" и вдумчивому математику. В данных случаях большую помощь может оказать ЭВМ как необходимый инструмент эффективного решения логических задач с многими переменными. В настоящее время нет ни одного языка программирования, который не включал бы логических операций.
Элементарные логические операции позволяют строить сложные (составные) высказывания на основе заданных высказываний.
Пусть X1, X2, X3, X4 - переменные высказывания (логические переменные), тогда следующие высказывания:
представляют формулы алгебры высказываний.
Так же, как и в алгебре арифметики, в алгебре логики устанавливается приоритет выполнения логических операций. Они упорядочены в следующей последовательности:
При этом отрицание является наиболее сильной операцией, эквивалентность - самой слабой. С учетом указанного порядка две формулы:
и
имеют одинаковые значения. Истинность составных высказываний (логических формул), образованных в результате выполнения логических операций над простыми высказываниями, зависит от истинности исходных высказываний. Для того, чтобы иметь возможность вычислять значения истинности этих высказываний, определим базовое понятие - логическую функцию.
Логические переменные и логические функции
Сущность алгебраического подхода к логике поясним на примере элементарной алгебры - алгебры арифметики. Основные объекты алгебры арифметики - выражения (формулы), состоящие из букв, знаков операций и скобок. С формулами производят процедуры двух типов: вычисления и преобразования.
Вычисления - вместо букв подставляют числа, знаки указывают действия, а скобки их порядок. Каждая формула задает функцию. Переменные - буквы формулы.
Преобразование формулы происходит так: исходная формула или ее часть F1 заменяется другой, в результате получается новая формула F2, которая эквивалентна F1 (т.е. при любых значениях аргументов F1 и F2 дают один и тот же результат). Преобразование выражений производится на основе законов арифметики, а также полученных из них соотношений.
По аналогии строится алгебра логики. Она рассматривает логические выражения как алгебраические, которые можно преобразовать по определенным правилам. Разница заключается в том, что в выражениях алгебры логики переменные являются логическими (0 и 1). Знаки операций обозначают логические операции (логические связки).
Логической функцией называется функция f (X1,X2,...,Xn ) , которая, так же как и ее аргументы, может принимать только два значения (0 и 1). Совокупность значений аргументов будем называть набором.
Любую логическую функцию можно задать таблицей истинности, в левой части которой вписаны все возможные наборы значений ее аргументов X1,X2,...,Xn , а правая часть - столбец значений функции, соответствующих этим наборам:
| № набора | X1,X2,...,Xn | f(X1,X2,...,Xn) |
|---|---|---|
| 0 | Набор значений аргументов | Значение функции (0 или 1) |
| 1 | ||
| ... | ||
| 2n - 1 |
Материал для изучения
Рекомендуемые ссылки
Список литературы
К разделу Вики-учебник для подготовки к ЕГЭ/Раздел Информатика/Основы логики
Назад к разделу Вики-учебник для подготовки к ЕГЭ/Раздел Информатика