Учебный проект Всегда на связи/четвёртая лекция математика

Учебный проект Всегда на связи

Вступление

Математический анализ - это раздел математики, изучающий функции и все, что с ними связано (скорость изменения - производная, площадь под кривой - интеграл, а также особые свойства функций). С появлением таких областей науки, как кинематика точки, термодинамика, теория вероятности, и т.д. появилась потребность в более тщательном анализе зависимостей: нахождение их максимумов, минимумов, точек перегиба кривых, нулей, промежутков возрастания и убывания и прочих сложных вещей.

Задачи, приводящие к понятию производной

В математике, физике и некоторых других науках есть проблемы, которые невозможно разрешить без взятия производной. Вот некоторые из них: важнейшей задачей было отыскали уравнения касательной к кривой в данной точке, кроме того, существует ряд других задач, таких как вычисление мгновенной скорости (ускорения, рывка) по уравнению на координату, или нахождение максимума функции. Фактически, во всех этих задачах целью было нахождения скорости изменения функции.

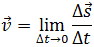
Задача о мгновенной скорости

Науке очень давно был технический способ отыскания средней скорости за конечный промежуток времени: вычисляется путь и делится на время. Так вот. Мгновенная скорость (по определению) есть средняя скорость за бесконечно короткий промежуток времени. Математически это осуществляет следующим образом рассматривается отношение приращения радиуса-вектора (перемещение) к приращению времени, а затем последнее устремляется к нулю: 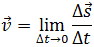. Такой предел называется мгновенной скоростью (или первой производной координат по времени) и обозначается либо значком радиуса вектора с штрихом или точкой наверху, либо в виде дроби (при этом, эту дробь не стоит воспринимать как отношение - это единый, цельный символ!): 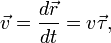. О том, как это посчитать, чуть ниже.

Определение производной

На основе только что сделанных соображений, дадим строго математическое определение производной.

Источники

• Артемий Марченко;
• Алексей Бычков