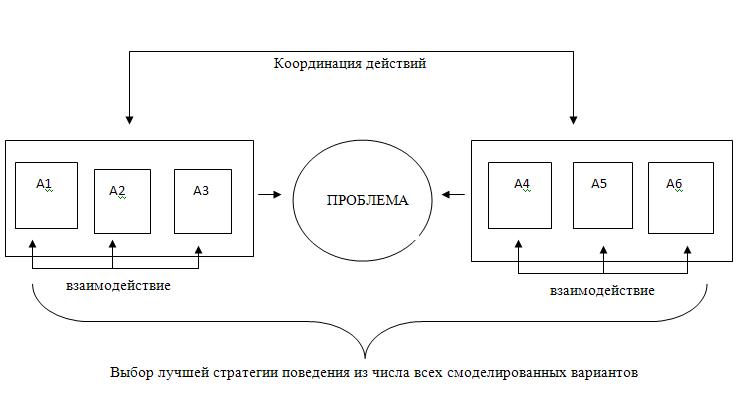
Модели взаимодействия в мультиагентных средах
| Строка 68: | Строка 68: | ||
--[[Участник:Алексей Крашенинников|Крашенинников Алексей]] ([[Обсуждение участника:Алексей Крашенинников|обсуждение]]) 21.58, 5 апреля 2016 (MSK) | --[[Участник:Алексей Крашенинников|Крашенинников Алексей]] ([[Обсуждение участника:Алексей Крашенинников|обсуждение]]) 21.58, 5 апреля 2016 (MSK) | ||
| + | |||
| + | [[Категория:ФС-13]] | ||
| + | |||
| + | '''Имитационное моделирование''' | ||
| + | |||
| + | В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории – неограниченно большое) число факторов. Но и у них – свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб. | ||
| + | Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей. | ||
| + | Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время . Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т.д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучивается принимать правильные решения – если не оптимальные, то почти оптимальные. | ||
| + | В современной литературе не существует единой точки зрения по вопросу о том, что понимать под имитационным моделированием. Так существуют различные трактовки: | ||
| + | - в первой – под имитационной моделью понимается математическая модель в классическом смысле; | ||
| + | - во второй – этот термин сохраняется лишь за теми моделями, в которых тем или иным способом разыгрываются (имитируются) случайные воздействия; | ||
| + | - в третьей – предполагают, что имитационная модель отличается от обычной математической более детальным описанием , но критерий, по которому можно сказать, когда кончается математическая модель и начинается имитационная , не вводится; | ||
| + | |||
| + | Имитационное моделированием применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или иные решения, подобно тому, как шахматист глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки, в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее текущее решение принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные. | ||
| + | |||
| + | '''Этапы процесса построения математической модели сложной системы''' | ||
| + | |||
| + | 1. Формулируются основные вопросы о поведении системы, ответы на которые мы хотим получить с помощью модели. | ||
| + | 2. Из множества законов, управляющих поведением системы, выбираются те, влияние которых существенно при поиске ответов на поставленные вопросы. | ||
| + | 3. В пополнение к этим законам, если необходимо, для системы в целом или отдельных ее частей формулируются определенные гипотезы о функционировании. | ||
| + | Критерием адекватности модели служит практика. | ||
| + | |||
| + | Трудности при построении математической модели сложной системы: | ||
| + | |||
| + | - Если модель содержит много связей между элементами, разнообразные нелинейные ограничения, большое число параметров и т. д. | ||
| + | - Реальные системы зачастую подвержены влиянию случайных различных факторов, учет которых аналитическим путем представляет весьма большие трудности, зачастую непреодолимые при большом их числе; | ||
| + | - Возможность сопоставления модели и оригинала при таком подходе имеется лишь в начале. | ||
| + | |||
| + | Эти трудности и обуславливают применение имитационного моделирования. | ||
| + | |||
| + | Оно реализуется по следующим этапам: | ||
| + | |||
| + | 1. Как и ранее, формулируются основные вопросы о поведении сложной системы, ответы на которые мы хотим получить. | ||
| + | 2. Осуществляется декомпозиция системы на более простые части-блоки. | ||
| + | 3. Формулируются законы и «правдоподобные» гипотезы относительно поведения как системы в целом, так и отдельных ее частей. | ||
| + | 4. В зависимости от поставленных перед исследователем вопросов вводится так называемое системное время, моделирующее ход времени в реальной системе. | ||
| + | 5. Формализованным образом задаются необходимые феноменологические свойства системы и отдельных ее частей. | ||
| + | 6. Случайным параметрам, фигурирующим в модели, сопоставляются некоторые их реализации, сохраняющиеся постоянными в течение одного или нескольких тактов системного времени. Далее отыскиваются новые реализации. | ||
| + | |||
| + | '''Метод Монте-Карло как разновидность имитационного моделирования''' | ||
| + | |||
| + | Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955—1956гг. | ||
| + | Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т. е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины' вручную—очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ. | ||
| + | Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. | ||
| + | Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас». | ||
| + | Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс — явно немарковскпй, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным). | ||
| + | В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 — (1/2)3 = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб—за попадание, решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен. | ||
| + | |||
| + | '''Список литературы''' | ||
| + | |||
| + | 1. Вентцель Е.С. «Исследование операций», Москва «Советское радио» 1972 г. | ||
| + | 2. Соболь И.М. «Метод Монте-Карло», Москва «Наука»,1985 г. | ||
| + | 3. «Экономико-математические методы и прикладные модели», под ред. Федосеева В.В. , Москва «Юнити» 2001 г. | ||
| + | |||
| + | --[[Участник:Кузнецова катя|Кузнецова катя]] | ||
[[Категория:ФС-13]] | [[Категория:ФС-13]] | ||
Версия 22:26, 5 апреля 2016
Мультиагентное моделирование при принятии управленческого решения. Мультиагентное моделирование является эффективным средством нахождения оптимального решения задач, принятия управленческого решения. В этом контексте та или иная ситуация проецируется на искусственно созданную модель, где каждый агент наделяется определенным функционалом. В управленческой среде речь может идти о моделировании ситуации, где задействованы люди, производственные процессы, объекты и прочее. Живые агенты — люди — имеют одно отличительное свойство по сравнению с другими агентами (роботы, компьютерные агенты). Это свойство — социальность. В таких моделях важно учитывать социальный статус, социальные отношения, распределение функций, наделение полномочиями. Агентные системы, смоделированные по образу человеческого сообщества, связаны с теорией организацией, теорией административного управления, теорией игр и др. Однако, в таких системах очень тяжело учесть ценностные ориентиры, которые приняты в данной группе. Люди могут выбрать нормативную и ненормативную линию поведения, что нельзя никак перенести на агент. Но в остальном агенты также могут обращаться к другим агентам при решении поставленной задачи, строить совместные планы, координировать свои действия. Такой подход к решению задачи очень удобен, он отсекает много рисков. Например, он позволяет руководителю выбрать правильную стратегию поведения во взаимоотношениях с поставщиками, клиентами, конкурентами, в кризисной ситуации ограниченности ресурсов. Если резюмировать, то при моделировании мультиагентных сред важно учитывать: 1. Отражение особенностей таких как, тип ресурса, с которым работают агенты (материальный, информационный, человеческий), состояние операции, проблемное поле; 2. Определение целей каждого агента, описание его знаний; 3. Описание механизма взаимодействия между агентами, группами агентов; 4. Описание механизма разрешения конфликтных ситуаций между агентами, группами агентов; 5. Описание плана действий агентов, групп агентов.
--Гнетнева Ксения (обсуждение) 13:55, 5 апреля 2016 (MSK)
Мультиагентное моделирование в среде NetLogo
Программа NetLogo обладает простым функциональным интерфейсом. Главным элементом, которого является окно «виртуального Мира» агентов. На рисунке это окно расположено в центре экрана.
Пользователь и разработчик агентной программы может взаимодействовать с ней в интерактивном режиме, подавая команды в окне «Командного центра», оно расположено в нижней части окна программы. Команды подаются на уровне определенного объекта программы моделирования: «Наблюдатель», «Пятна», «Черепахи» (агенты), «Связи». Команда — это определенный оператор языка программирования NetLogo. Допускается создание комбинированных моделей, код которых предварительно записан на языке NetLogo, и затем модель исследуется с привлечением командного центра. Код агентной модели представляет собой набор процедур. Пример на картинке:
В модели всегда должны присутствовать две процедуры setup и go [4]. Первая процедура связывается с командной кнопкой инициализации агентов модели, вторая запускает процесс моделирования. Движение агентов в виртуальном мире показано на рисунке. По умолчанию используется пиктограмма агента в виде направленного острия. Допускается сменить пиктограмму агента на другую из библиотеки ресурсов программы, либо создать собственную пиктограмму, с помощью графического редактора. Графический редактор входит в систему моделирования.
Примером модели может служить — Модель «хищник — жертва»
Такой класс моделей позволяет исследовать взаимодействие агентов в виртуальном Мире, где наблюдается конкуренция между агентами. Один класс агентов «хищники», поддерживают свой жизненный потенциал за счет уничтожения других агентов «жертв». Вид интерфейса работающей модели показан на рисунке
Агенты обоего типа обладает энергией, если она падает ниже определенного уровня, то агент «умирает». Агенты жертвы поддерживают свою энергию за счет «зеленых пятен», поглощая их, агент хищник поддерживает свою энергию за счет уничтожения жертв. Когда энергия агентов возрастает до определенного уровня, они воспроизводит себе подобных. Это операция клонирования агентов. Для контроля за состоянием ресурсов используется экран «Ресурсы». Экран отображает число ресурсов — пятен зеленого цвета, ресурсы возобновляются. Из рисунка видно, что популяции «хищников» и обычных агентов имеет пиковые значения, после численность популяции начинает стабилизироваться.
--Крашенинников Алексей (обсуждение) 21.58, 5 апреля 2016 (MSK)
Имитационное моделирование
В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению, с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории – неограниченно большое) число факторов. Но и у них – свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходятся искать «на ощупь», путем догадок и проб. Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей. Аналитическая модель дает возможность в общих чертах разобраться в явлении, наметить как бы контур основных закономерностей. Любые уточнения могут быть получены с помощью статистических моделей. Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или другие решения, подобно тому, как шахматист, глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время . Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т.д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучивается принимать правильные решения – если не оптимальные, то почти оптимальные. В современной литературе не существует единой точки зрения по вопросу о том, что понимать под имитационным моделированием. Так существуют различные трактовки: - в первой – под имитационной моделью понимается математическая модель в классическом смысле; - во второй – этот термин сохраняется лишь за теми моделями, в которых тем или иным способом разыгрываются (имитируются) случайные воздействия; - в третьей – предполагают, что имитационная модель отличается от обычной математической более детальным описанием , но критерий, по которому можно сказать, когда кончается математическая модель и начинается имитационная , не вводится;
Имитационное моделированием применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек, руководящий операцией, может в зависимости от сложившейся обстановки, принимать те или иные решения, подобно тому, как шахматист глядя на доску, выбирает свой очередной ход. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки, в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее текущее решение принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные.
Этапы процесса построения математической модели сложной системы
1. Формулируются основные вопросы о поведении системы, ответы на которые мы хотим получить с помощью модели. 2. Из множества законов, управляющих поведением системы, выбираются те, влияние которых существенно при поиске ответов на поставленные вопросы. 3. В пополнение к этим законам, если необходимо, для системы в целом или отдельных ее частей формулируются определенные гипотезы о функционировании. Критерием адекватности модели служит практика.
Трудности при построении математической модели сложной системы:
- Если модель содержит много связей между элементами, разнообразные нелинейные ограничения, большое число параметров и т. д. - Реальные системы зачастую подвержены влиянию случайных различных факторов, учет которых аналитическим путем представляет весьма большие трудности, зачастую непреодолимые при большом их числе; - Возможность сопоставления модели и оригинала при таком подходе имеется лишь в начале.
Эти трудности и обуславливают применение имитационного моделирования.
Оно реализуется по следующим этапам:
1. Как и ранее, формулируются основные вопросы о поведении сложной системы, ответы на которые мы хотим получить. 2. Осуществляется декомпозиция системы на более простые части-блоки. 3. Формулируются законы и «правдоподобные» гипотезы относительно поведения как системы в целом, так и отдельных ее частей. 4. В зависимости от поставленных перед исследователем вопросов вводится так называемое системное время, моделирующее ход времени в реальной системе. 5. Формализованным образом задаются необходимые феноменологические свойства системы и отдельных ее частей. 6. Случайным параметрам, фигурирующим в модели, сопоставляются некоторые их реализации, сохраняющиеся постоянными в течение одного или нескольких тактов системного времени. Далее отыскиваются новые реализации.
Метод Монте-Карло как разновидность имитационного моделирования
Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955—1956гг. Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т. е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины' вручную—очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ. Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас». Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс — явно немарковскпй, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным). В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 — (1/2)3 = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб—за попадание, решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен.
Список литературы
1. Вентцель Е.С. «Исследование операций», Москва «Советское радио» 1972 г. 2. Соболь И.М. «Метод Монте-Карло», Москва «Наука»,1985 г. 3. «Экономико-математические методы и прикладные модели», под ред. Федосеева В.В. , Москва «Юнити» 2001 г.