Учебный проект Всегда на связи/четвёртая лекция математика
| Строка 1: | Строка 1: | ||
| − | + | ===Начало анализа. Производные=== | |
[[Учебный проект Всегда на связи]] | [[Учебный проект Всегда на связи]] | ||
Текущая версия на 06:54, 31 июля 2014
[править] Начало анализа. Производные
Учебный проект Всегда на связи
[править] Вступление
Математический анализ - это раздел математики, изучающий функции и все, что с ними связано (скорость изменения - производная, площадь под кривой - интеграл, а также особые свойства функций). С появлением таких областей науки, как кинематика точки, термодинамика, теория вероятности, и т.д. появилась потребность в более тщательном анализе зависимостей: нахождение их максимумов, минимумов, точек перегиба кривых, нулей, промежутков возрастания и убывания и прочих сложных вещей.
[править] Задачи, приводящие к понятию производной
В математике, физике и некоторых других науках есть проблемы, которые невозможно разрешить без взятия производной. Вот некоторые из них: важнейшей задачей было отыскали уравнения касательной к кривой в данной точке, кроме того, существует ряд других задач, таких как вычисление мгновенной скорости (ускорения, рывка) по уравнению на координату, или нахождение максимума функции. Фактически, во всех этих задачах целью было нахождения скорости изменения функции.
[править] Задача о мгновенной скорости
Науке очень давно был технический способ отыскания средней скорости за конечный промежуток времени: вычисляется путь и делится на время. Так вот. Мгновенная скорость (по определению) есть средняя скорость за бесконечно короткий промежуток времени. Математически это осуществляет следующим образом рассматривается отношение приращения радиуса-вектора (перемещение) к приращению времени, а затем последнее устремляется к нулю: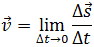 
. Такой предел называется мгновенной скоростью (или первой производной координат по времени) и обозначается либо значком радиуса вектора с штрихом или точкой наверху, либо в виде дроби (при этом, эту дробь не стоит воспринимать как отношение - это единый, цельный символ!): 
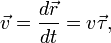. О том, как это посчитать, чуть ниже.
[править] Определение производной
На основе только что сделанных соображений, дадим строго математическое определение производной. Производной функции f(х) по переменной х в точке х0 называется такая функция f'(x), что:
Обозначается производная следующим образом:
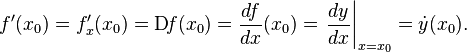
[править] Вычисление производных
Вычисление производных производится согласно определению через предел. Покажем это на примере производной степенной функции:
1. Найдем общий вид приращения степенной функции:
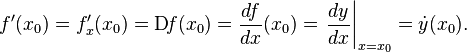
2. Запишем отношение приращения функции к приращению своего аргумента и сосчитаем предел:
.
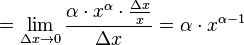Тот же результат можно получить и по-другому, аккуратно раскрыв выражение типа "n-ная степень суммы" и почленно разделив результат на приращение аргумента, затем воспользовавшись аддитивным свойством пределов (предел суммы равен сумме пределов). После этого станет видно, что все слагаемые, кроме одного, благополучно убиваются, а остается только требуемый результат.
[править] Производные высших порядков
Иногда в математике и физике нужны зависимости, которые носили бы смысл скорости изменения скорости изменения функции. Такие вещи по своей прироле являются производной производной функции и называются производными второго порядка. (При желании, можно получить и производные третьего, пятого, сотого порядков). Обозначаются они так:
И имеют физический смысл ускорения (если первоначальной функцией была временная функция радиус-вектора).
[править] Некоторые приложения производной к анализу функции
Если на каком-то отрезке производная функции положительна, это вовсе не значит, что функция расположена выше оси абсцисс - нет, это значит лишь, что функция растет. Наоборот, если производная отрицательна, то это значит, что исходная функция падает. Также, равенство нулю производная означает, что при данном значении аргумента функция испытывает экстремум. Аналогично, если вторая производная положительна, то функция "выгнута" в сторону положительного направления оси ординат. И наоборот, если вторая производная отрицательна, то функция вогнута. Также, равенство нулю второй производной бывает в точке перегиба исходной функции.
[править] Таблица производных
Чтобы каждый раз не считать предел, математики разработали своеобразный сборник производных элементарных функций (составлялся он все так же вручную, подсчетом пределов). Вот эта таблица:
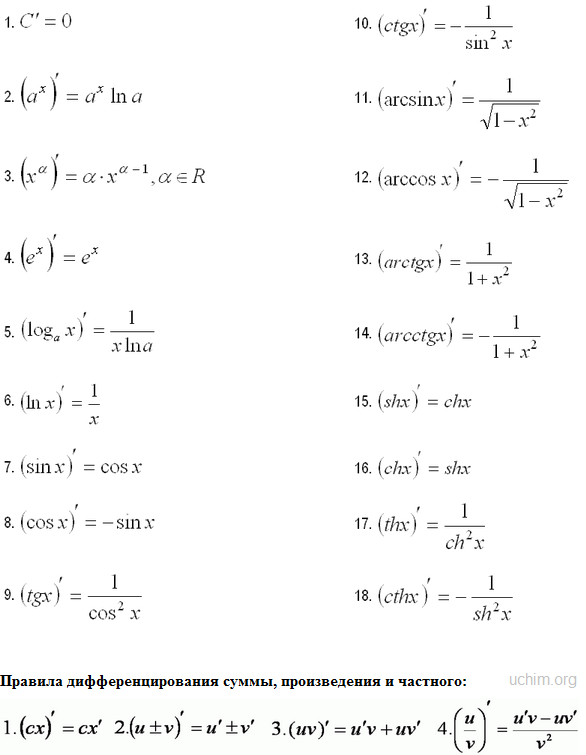
[править] Дифференцирование сложной функции
Производную имеет почти любая функция (даже неэлементарная). В том числе, функционалы и сложные функции (то есть, такие зависииости, аргументами которых тоже являются функции). Их производные берутся согласно ряду правил, которые находятся под таблицей производных.
[править] Примеры
Дифференцирование (в отличие от обратной ей операции) - очень простая штука. Делается все примерно так: смотри в таблицу, подставляй, пиши, повторить. Таким образом,
Производная квадратичной функции является функция вида y'(x)=2ax. Линейная функция растет со скоростью y=ax, и т.д.. Примеры взятия производной громоздкой функции:
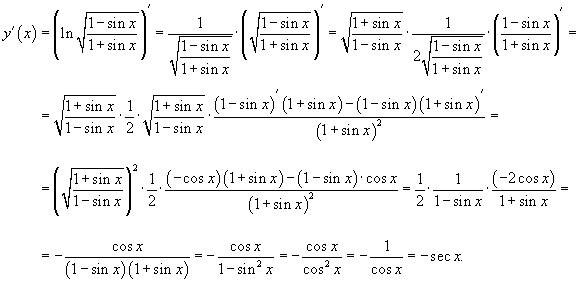
[править] Геометрический и физический смысл производной
Производная, по опеределению, есть отношение малого приращения функции к малому приращению аргумента. Тогда можно рассмотреть бесконечно маленький прямоугольный треугольничек с катетами dy (вертикальный) dx (горизонтальный). Тогда dy/dx есть ни что иное как тангенс угла наклона касательной в заданной точке. Это и есть геометрический смысл производной.
Физический смысл производной связан с функциями времени, в частности, с вычислением мгновенной скорости точки в заданный момент времени и звучит примерно так: производная временной функции есть скорость ее роста.
[править] Применения производной
[править] Вычисление экстремумов
Очевидно, что в экстремуме функция не растет (на то он и экстремум). Берем производную, требуем, чтобы она была равна нулю, решаем уравнение, находим аргумент и подставляем его в функцию. Все.
[править] Вычисление точек перегиба
Тот же алгоритм, что с экстремумами, только вместо первой производной берется вторая.
[править] Построение графиков функций
Пожалуй, самая нужная функция производной. Вычисляя соответственно первую и вторую производные на разумно выбранных интервалах области определения можно легко угадать форму графика функции. Очень удобный и быстрый метод построения графиков.
[править] Обобщения понятия производной
[править] Частная производная
Существует обобщения производной на случай функции нескольких аргументов - так называемая частная производная.
[править] Правая и левая производные
Если у функции нет производной в одной точке (модуль, скажем), то считают производную слева и справа соответственно. Так, у функции y=|x| в нуле производной нет, зато есть левая (-1) и правая (1).
[править] Лагранжевы производные
Довольно сложное понятие. Они действуют на функции аж трех, а то и четырех аргументов - на так называемые поля. Их всего три: градиент, дивергенция и вихрь(ротор). Градиент является, по сути своей, производной по направлению и представляет собой вектор, который смотрит в стороны скорейшего возрастания поля. Дивергенция - количественная характеристика векторного поля, показывающая, насколько больше в данную область поля втекает, чем вытекает. Так, если дивергенция в данной точке положительна, то эта точка - источник, если отрицательна - то сток. Ротор же показывает, насколько сильно векторное поле закручено.
[править] Заключение
Производная, будучи простейшим понятием дифференциального исчисления, может быть очень и очень полезна и удобна в применении. Теперь, становится очевидно, что более общие и сложные понятия этого раздела математического анализа, приносят еще больше пользы. Чуть позднее после введения производной математикам пришла в голову идея составлять уравнения, связывающие функцию и скорость ее изменения, дифференциальные уравнения. Более того, такие уравнения научились решать, что позволило ученым решать задачи на многие порядки сложнее. В том числе, после того, как Исаак Ньютон доказал точность и применимость своей теории гравитации только решая такие уравнения, стало очевидно: "Все физические процессы в мире описываются дифференциальными уравнениями" (И.Ньютон).
[править] Источники
- Артемий Марченко;
- Алексей Бычков
